การเก็บเลขทศนิยมในคอมพิวเตอร์ ด้วย IEEE 754

บทนำเกี่ยวกับเรื่องการเก็บตัวเลข

หลายๆ คนคงรู้อยู่แล้วว่าเวลาคอมพิวเตอร์เก็บเลขฐาน 10 ที่ใช้กันในชีวิตประจำวัน มันเก็บยังไงและนำไปใช้ต่อยังไง เพราะเราก็แค่แปลงเลขที่ได้มาเป็นฐาน 10 เป็นฐาน 2 เพื่อให้เก็บค่าลงบิตต่างๆ ในคอมพิวเตอร์ได้ เช่นจาก $6_{10}$ เป็น $110_2$ มันก็แค่นี้ใช่มั้ยล่ะ

แต่ทีนี้ถ้าเราจะมาดูในเคสที่เก็บทศนิยมกันบ้าง ถ้าจะเก็บ $1.25_{10}$ เป็นเลขฐาน 2 ถ้าเราลองใช้หลักการคล้ายๆ เลขฐาน 10 ในส่วนทศนิยมเหมือนกัน
ก็จะได้ว่าเก็บเป็น $1.01_{2}$ ก็คือ $1\times2^0+0\times2^{-1}+1\times2^{-2} = 1.25_{10}$

โอเคแล้วทีนี้จะเก็บลงคอมยังไงดีล่ะ?

สังเกตว่าถ้าใช้การเก็บข้อมูล 32 บิตแบบคล้ายๆกับการเก็บจำนวนเต็ม

ถ้าสนใจเฉพาะค่าบวก (ไม่ติดลบ) เราก็อาจจะลองแบ่ง 16 บิต ไปใช้ในการเก็บส่วนจำนวนเต็ม แล้วก็เอาอีก 16 บิต ที่เหลือไปเก็บส่วนทศนิยม เราก็จะเก็บค่าได้ตั้งแต่ $0 - (65536-2^{-16})$

เพราะ 16 บิตที่เป็นเลขจำนวนเต็มสามารถเก็บค่าได้ถึง $65535$ ส่วนฝั่งทศนิยมเก็บได้ถึง $1 - 2^{-16}$

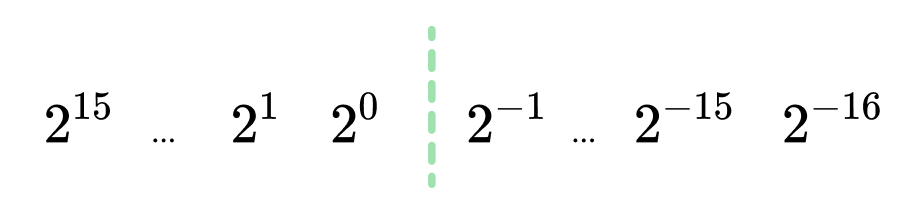มีอาเรย์สี่เหลี่ยมอยู่ 32 ช่องที่โดนเส้นแบ่งครึ่งตรงกลางกลายเป็น 16 ช่องทั้งคู่ โดยที่ฝั่งซ้ายได้สองยกกำลังสิบห้าไปจนถึงสองยกกำลังศูนย์ และที่เหลือทางขวาค่อยๆไล่จากยกกำลัง -1 ไปเรื่อยๆ รูปแสดงลักษณะการเก็บเลขฐานสองบนระบบทศนิยม

ซึ่งก็นอกจากจะเก็บค่าได้ในช่วงที่มีค่าไม่เยอะ แถมยังมีปัญหาต่อมาในเรื่องความแม่นยำอีก เพราะเก็บความละเอียดสูงสุดไหวแค่ $2^{-16}$

ดูตัวอย่างนิดหน่อย

ระบบเลขฐาน 2 แบบนี้จะเก็บค่าบางอย่างไม่ได้ เช่น $0.3_{10}$ จะเก็บค่าได้ใกล้เคียงสุดคือ $0.0100110011001100_2 \approx 0.299988$ ซึ่งก็มีความคลาดเคลื่อนไปหน่อยนึง (ที่ก็ยังเยอะอยู่ดี)

ทำให้ถ้าอยากจะเพิ่มความแม่นยำในส่วนทศนิยมให้ค่าผิดไม่เกิน $2^{-x}$ เราต้องใช้เลขในส่วนทศนิยม $x$ บิต ซึ่งถ้าต้องการความแม่นยำมากๆ เราก็จะเสียจำนวนบิตไปในส่วนนี้เยอะมาก และทำให้จำนวนบิตที่เหลือที่จะเป็นเก็บส่วนจำนวนเต็มมีน้อยลง ก็แปลว่าค่าสูงสุดที่เก็บได้ก็จะน้อยลงด้วย

และอีกอน่างที่สำคัญคือ ในตอนแรกๆ ยังไม่มีมาตรฐานที่ตกลงร่วมกัน (ว่าง่ายๆ คือ ใครอยากทำอะไรก็ทำไป อยากใช้กี่บิตก็เอาเลย) ก็เลยทำให้ต้องมีการตกลงมาตรฐานร่วมกันเพื่อให้มีรูปแบบการใช้งานชัดเจนขึ้น เลยเกิดเป็นมาตรฐาน IEEE 754 ขึ้นมา

IEEE 754

ด้วยความที่การเก็บเลขทศนิยมเป็นปัญหากันมานาน แล้วแต่ละที่ก็เก็บไม่เหมือนกันสักแบบ

ทาง Institute of Electrical and Electronics Engineers (IEEE) ก็เลยมีการสร้างมาตรฐานชื่อว่า IEEE 754 ในการเก็บเลขทศนิยมเพื่อให้เป็นสากลและใช้เหมือนกันทุกที่ ซึ่งก็คล้ายๆกับสัญกรณ์วิทยาศาสตร์ที่เคยๆเห็นกันนั่นแหละ

ซึ่งก็จะได้ลักษณะประมาณนี้

a \times10^b

แต่ด้วยความที่คอมมันไม่ได้เก็บเป็นฐาน 10 ก็เลยเขียนเป็นฐาน 2 แทน

a \times2^b

ทำให้เวลาเก็บค่า เราแก้ปัญหาเรื่องความแม่นยำได้ผ่านทางการกำหนดค่าเลขที่คูณนำหน้า ( $a$ ) และกำหนดช่วงของค่าให้ครอบคลุมค่าใหญ่ๆ ได้ผ่านการปรับเลขชี้กำลัง ( $b$ )

ทีนี้พอเราจะเก็บค่าติดลบด้วย เราก็จะเพิ่มอีก 1 บิต มาเก็บว่าเป็นค่าบวกหรือลบ ทำให้รูปแบบการเก็บเลขเป็นแบบนี้แทน

(-1)^{Sign} \times a \times 2^{b}

ทำให้วิธีการเก็บเลขทศนิยมตามมาตรฐาน IEEE 754 เลยจะมี 3 ส่วนหลักๆ:

Sign Bit (1 บิต): เก็บว่าเป็นค่าบวก หรือค่าลบ
Exponent (8 บิต): เก็บเลขชี้กำลัง (ค่า $b$ )
Mantissa (23 บิต): เลขบอกค่าความละเอียด (ค่า $a$ )

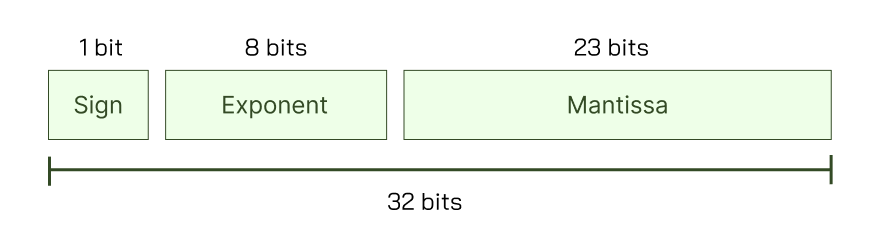รูปวาดตารางช่องบิตทั้งหมด 32 ถูกแบ่งเป็น 3 ส่วนที่มีชื่อว่า Sign, Exponent และ Mantissa ลักษณะการจัดเรียงบิตของ IEEE 754 ทั้ง 32 บิต

ส่วนตอนที่คอมเอาไปประมวลผลจะใช้ format เป็นว่า

(-1)^{Sign} \times (1.\text{mantissa}) \times 2^{\text{Exponent - 127}}

แต่ก็อาจจะงงๆอยู่ดีว่าทำไมต้อง $1.\text{mantissa}$ กับ $2^{\text{Exponent} - 127}$ ใช้ตรงๆเลยไม่ได้หรอ?

อะไรคือ 1.Mantissa ?

เหมือนตอนเราเรียนเรื่องสัญกรณ์วิทยาศาสตร์แหละ เลขๆนึงมันเขียนได้หลายแบบ เช่น

\begin{aligned} 1234 & = 123.4 \times 10^1 \\ & = 12.34 \times 10^2 \\ & = 1.234 \times 10^3 \\ \end{aligned}

และด้วยความที่มันไม่แน่นอนว่ามันจะเขียนยังไงดี เพื่อความเป็นระบบเขาก็จะอยากให้เป็นแบบสุดท้าย ( $1.234 \times10^3$ ) ซะมากกว่า

ตอนเราจะเก็บเลขฐาน 2 ก็เหมือนกัน แทนที่เราจะต้องมาเก็บว่า $0.010011_2$ มีบิตแรกเป็น $0$ แล้วค่อยๆไล่ต่อไปเรื่อยๆ ทำไมเราไม่ทำให้บิตแรก (บิตหน้า .) เป็น $1$ ไปเลยล่ะ?

จากที่เรามี $0.010011_2$ ก็เปลี่ยนมันเป็น $1.0011_2 \times 2^{-2}$ ไปเลยสิ แถมถ้าตัวหน้ารับประกันว่าเป็น $1$ อยู่แล้วด้วย เราก็ไม่ได้จำเป็นต้องเก็บมันอีก

ก็แปลว่าเราจำเป็นแค่เก็บตัวหลังจาก . ก็พอแล้ว การเก็บ Mantissa ก็ทำแบบนั้นแหละ ทุกบิตใน Mantissa ก็เลยใช้แทนเลขหลัง $1.$ ทั้งหมดไปเลย

เราเลยได้ว่า $1.\text{Mantissa}$ เป็นตัวบอกค่าความละเอียดของเลขทศนิยม

ทำไมต้อง Exponent-127?

ทีนี้อีก 8 บิตที่เหลือที่เอาไปทำ Exponent เอาไปทำอะไรล่ะ?

เราพอรู้แหละว่า 8 บิตนี้ถ้าจะเก็บเป็นจำนวนเต็ม จะเก็บเลขได้ตั้งแต่ (0-255) แต่จากตัวอย่างตอนอธิบายเรื่อง Mantissa เมื่อกี้เราก็เห็นแล้วว่า Exponent ติดลบมันก็จำเป็น ไม่งั้นจะใช้แทนค่าที่มีค่าน้อยๆยังไง?

ค่าของ Exponent ก็ต้องเอามาลบ Bias (127) ออกก่อนเพื่อให้เรามี Exponent ทั้งค่าบวกและลบที่ครอบคลุมเท่าๆกัน

แล้วเลขที่เจอบ่อย ๆ อย่าง 0 และตัวอื่นล่ะ?

ถ้าดูจากรูปแบบการเก็บค่า จะเห็นว่าเวลาจะเรียกใช้ค่า 0 นั้นจะทำไม่ได้เลยเพราะในส่วนของ Exponent-127 นั้นไม่มีทางทำให้เป็น 0 ได้ ซึ่งค่าที่ใกล้ที่สุดคือประมาณ $2^{-127}$ (หรือก็คือทุก bit ในส่วน Exponent-127 เป็น 0 หมด) และ 0 ก็ดันเป็นค่าที่เจอบ่อยมาก ๆ ด้วย

พอรวมกับค่าอื่น ๆ ที่เจอกันบ่อยๆ เช่น $\infty$ , NaN ก็เลยทำให้มีการสร้างเงื่อนไขพิเศษขึ้นมาเพื่อให้คอมมันรู้ว่าถ้ากำหนดค่าแบบนี้ จะเป็นค่าพิเศษนะอะไรประมาณนั้น ตัวอย่างเช่น

ถ้าจะแทนค่า 0 จะให้ bit ในส่วน Exponent และ Mantissa เป็น 0 ให้หมดเลย ส่วน Sign bit จะเป็น 0 หรือ 1 ก็ได้
ส่วนค่าอย่าง $\pm$ $\infty$ จะใช้ bit ในส่วน Exponent เป็น 1 ทั้งหมดและ Mantissa เป็น 0 ทั้งหมด ส่วน Sign bit จะขึ้นตามเครื่องหมาย
และ NaN ก็จะใช้ bit ในส่วน Exponent เป็น 1 ทั้งหมดและให้ Mantissa มีค่าไม่เท่ากับ 0 เพื่อที่จะแยกว่าไม่ใช่ $\pm$ $\infty$

สรุป

กลับมาที่ค่า $0.3_{10}$ ถึงเราจะใช้ IEEE 754 มันก็ยังไม่ได้ช่วยให้เราเก็บมันได้แบบเป๊ะๆอยู่ดี จาก format การเก็บข้อมูลของ Floating-point จะเห็นได้ว่าความคลาดเคลื่อนขึ้นจะอยู่กับส่วนของ Exponent-127

ถ้ายิ่งค่าน้อยก็จะมีความคลาดเคลื่อนน้อยมากๆ แต่ถ้ายิ่งค่ามาก ความคลาดเคลื่อนก็จะมากเหมือนกัน เพราะตัว Mantissa ก็เก็บความละเอียดได้แค่ประมาณนึง ซึ่งมันก็คลาดเคลื่อนบ้างอยู่แล้ว แล้วยังมี $2^{\text{Exponent} - 127}$ มาคูณตามหลังอีก

ดังนั้นไม่ว่าจะทำ operation อะไรบนเลข Floating-point ก็ต้องเผื่อค่าความคลาดเคลื่อนไว้ตลอด อย่างน้อยๆสัก 0.00001 ก็ยังดี เพราะถ้าปล่อยไปเลยก็จะได้ลักษณะเหมือนใน Meme ที่มันเป็นแบบนี้

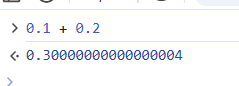ภาพหน้าจอโค้ดที่รันบนเบราว์เซอร์ว่า 0.1 + 0.2 ที่ได้ค่าเกิน 0.3 ตัวอย่างความคลาดเคลื่อนใน IEEE 754

แชร์หน่อยก๊าบ ⊹

คัดลอกแล้ว!