เฉลยโจทย์จาก Contest CodeAlgo 2025 ฉบับสั้นๆ

บันไดงูอย่างง่าย (Snake and Ladder Trial Edition)

https://github.com/Practical-Algorithm/Contests/blob/main/CodeAlgo2025/Code_Algo_2025-snake1.pdf

ข้อนี้เป็นการเริ่มเดินจากช่องที่ 1 ไปให้ถึงช่องที่ $N$ โดยให้เดินน้อยครั้งที่สุด ซึ่งการเดินให้น้อยที่สุดก็แปลว่า แต่ละครั้งที่เดินก็ต้องไปให้ได้หลายช่องมากที่สุดเหมือนกัน

ดังนั้นจากช่องแรก ยังไงก็จะเดิน 5 ช่องก่อนเลยแน่ๆ และเมื่อเราลงที่ช่องที่ 6 เราก็จะสลับไปใช้ลูกเต๋าอีกลูกที่มีเลข 6 แล้ว หลังจากนั้นก็จะเดินแต่ 6 ช่องไปเรื่อยๆจนถึงเส้นชัย ทำให้ต้องเดินทั้งหมด $\lceil\frac{N}{6}\rceil$ ครั้ง เพราะเดินเลยเส้นชัยไปก็ได้

สามเหลี่ยมปาสคาล (Pascal Triangle)

โจทย์ข้อ 2 สามเหลี่ยมปาสคาล

https://github.com/Practical-Algorithm/Contests/blob/main/CodeAlgo2025/Code_Algo_2025-triangle.pdf

ก็เขียนตามโจทย์เลยนั่นแหละ ไม่ได้มีทริกอะไรเลย

จมน้ำ (Drown)

โจทย์ข้อ 3 จมน้ำ

https://github.com/Practical-Algorithm/Contests/blob/main/CodeAlgo2025/Code_Algo_2025-drown.pdf

ด้วยความที่ความสูงจะอยู่เท่าเดิมจนกว่าจะมีข้อมูลใหม่เข้ามา แทนที่เราจะต้องค่อยๆตรวจข้อมูลความสูงในทุกวินาทีตามที่โจทย์ให้มา เราก็ไปดูแค่วินาทีสุดท้ายก่อนที่ความสูงจะมีการเปลี่ยนแปลงก็ได้ เพราะถ้าคนใดคนหนึ่งจะจม จะคำนวณตอนวินาทีที่จมจริงๆ หรือวินาทีสุดท้ายก่อนความสูงเปลี่ยนก็ไม่ต่างกัน (เพราะจมอยู่ดีเนื่องจากน้ำมันขึ้นเรื่อยๆ)

ทำให้ถ้าเรามีข้อมูลชุดนึงว่าอยู่ที่ตำแหน่งความสูง 10 ตอนเวลา $x$ หน่วย และอยู่สูง 20 หน่วยตอนเวลา $y$ หน่วย เราก็แค่ดูว่าตอนเวลา $y-1$ หน่วยนั้น อยู่ที่ความสูง 10 ยังรอดอยู่ไหมก็พอ ซึ่งเราก็ทำแบบนี้ไปกับทุกคู่ชุดข้อมูลที่เรามี ของทุกๆคนก็ได้แล้ว

ตัวต่อ (Kindergarten Lego)

โจทย์ข้อ 4 ตัวต่อ

https://github.com/Practical-Algorithm/Contests/blob/main/CodeAlgo2025/Code_Algo_2025-lego.pdf

ก่อนอื่นต้องคิดก่อนว่าเราใส่ตัวต่อลงไปได้มากสุดกี่ตัว

ซึ่งวิธีใส่ให้ได้เยอะที่สุดคือการวางตัวต่อที่กินพื้นที่น้อยที่สุดเท่าที่เป็นไปได้โดยยังไม่ได้ไปทับกับใคร(หรือโดนอันอื่นทับ)

ถ้าลองสมมติว่าแผ่นกระดานเป็น ตารางขนาด $N \times N$ เราจะวางตัวขนาด $1 \times N$ ลงไปก่อน แล้วตามด้วย $2 \times (N-1)$ ไปเรื่อยๆจนถึงชิ้นที่มีขนาด $N \times 1$ เราจะได้ว่าใส่ได้มากสุดแค่ $N$ ชิ้นเท่านั้น

ถ้าเราใช้หลักการเดียวกันไปคิดกับตาราง $N \times M$ ก็จะได้คำตอบคล้ายๆกันคือใส่ได้ $\text{min}(N, M)$ ชิ้น

ทีนี้ลองมาคิดว่าจะแบ่งพื้นที่ให้ตัวยังไงดีหลังจากรู้ว่าจะวางกี่ชิ้นแล้ว

ลองดูตัวอย่างนี้นิดนึงลองกัน:

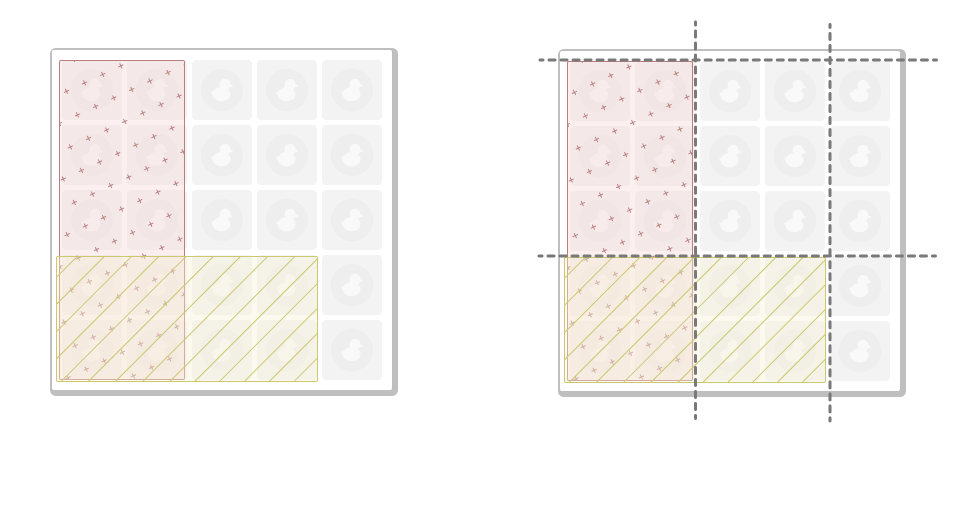การคำนวณว่าวางได้กี่แบบสามารถแปลงเป็นการลากเส้นบนสี่เหลี่ยมทั้งสองด้านได้

จะเห็นว่าจริงๆแล้ว เราแค่ต้องลากเส้นบนตารางเอง ซึ่งก็คำนวณได้ไม่ยากด้วย combinatoric

กลับบ้าน (Place to Call Home)

โจทย์ข้อ 5 กลับบ้าน

https://github.com/Practical-Algorithm/Contests/blob/main/CodeAlgo2025/Code_Algo_2025-home.pdf

เนื่องจากว่าแต่ละเขตเกี่ยวข้องกันกับแค่เขตที่อยู่ติดกันเท่านั้น แปลว่าตอนที่ดูว่าไปที่เขต $i$ ของแต่ละหมู่บ้านได้กี่วิธี เราก็จำเป็นต้องรู้แค่ว่าเรามาจากเขต $i-1$ ได้กี่วิธีก็พอ แต่ถึงอย่างนั้นก็ยังต้องรู้อยู่ดีว่าการที่เขต $i-1$ มันเดินมาได้กี่แบบ

ซึ่งข้อมูลจำนวนรูปแบบการเดิน เราสามารถเก็บข้อมูลด้วย matrix ได้ เช่น

\begin{bmatrix} 1\\ 1\\ \end{bmatrix}

เราสามารถแทนว่าตอนนี้เราสามารถเดินไปเมืองที่ 1 และ 2 ได้อย่างละ 1 วิธี

ทีนี้การจะคำนวณหาจำนวนวิธีของเขตถัดไปก็ทำได้โดยการดูว่าหมู่บ้านหนึ่งๆ สามารถมาจากหมู่บ้านไหนได้บ้างอย่างเช่นถ้าบอกว่าหมู่บ้านที่ 1 สามารถเดินทางจากหมู่บ้านที่ 1 หรือ 2 ก็ได้ คำตอบในเขตถัดไปก็จะเป็นการเอาจำนวนวิธีการเดินทางไปหมู่บ้านที่ 1 บวกกับของหมู่บ้านที่ 2 ซึ่งเราก็สามารถนำมาแปลงเป็น matrix เพื่อให้คำนวณทุกหมู่บ้านรวดเดียวได้แบบนี้:

\begin{bmatrix} 1 & 1\\ \_ & \_\\ \end{bmatrix}

เพื่อที่ว่าตอนคำนวณ

\begin{bmatrix} 1 & 1\\ \_ & \_\\ \end{bmatrix} \times \begin{bmatrix} 1\\ 1\\ \end{bmatrix} = \begin{bmatrix} 2\\ \_\\ \end{bmatrix}

พอมันมีหลายเขตเข้าหน่อยมันก็กลายเป็นว่าต้องคูณ matrix ที่ใช้คำนวณวิธีซ้ำๆหลายๆรอบ ก็เลยต้องทำการคำนวณ exponent แทน

\begin{bmatrix} 1 & 1\\ \_ & \_\\ \end{bmatrix} \times \dots\times \begin{bmatrix} 1 & 1\\ \_ & \_\\ \end{bmatrix} \times \begin{bmatrix} 1\\ 1\\ \end{bmatrix} = \begin{bmatrix} 1 & 1\\ \_ & \_\\ \end{bmatrix}^n \times \begin{bmatrix} 1\\ 1\\ \end{bmatrix}

โจทย์ก็เลยกลายเป็นการคำนวณ matrix แทน ที่เราก็ทำได้ด้วยเทคนิกชื่อ Fast Exponentiation เพื่อให้คำนวณได้เร็วขึ้น

บันไดงู (Snake and Ladder Super Ultra Deluxe)

โจทย์ข้อ 6 บันไดงู (Ultra Deluxe)

https://github.com/Practical-Algorithm/Contests/blob/main/CodeAlgo2025/Code_Algo_2025-snake2.pdf

เราจะมาดูว่าการหาค่าของคำถามเดียวนั้นทำยังไงกันก่อน

สมมติให้ $dp[i][j]$ เป็นแต้มที่ได้มากที่สุดจากการเดินทั้งหมด $i$ ครั้ง และเริ่มที่ช่องที่ $j$ เราจะได้ว่าถ้าเดินได้ $L$ ถึง $R$ ช่องแล้ว ค่าจะเป็น

dp[i][j] = \max(\max_{L\leq k \leq R} \{dp[i-1][j+k]\},dp[i-1][j])

ด้วยความที่เราต้องดูข้อมูลแค่ช่วงระหว่าง $L$ ถึง $R$ เราสามารถใช้ Monotonic Queue ในการไล่เก็บว่าช่องไหนที่มีค่ามากที่สุดในช่วงๆนั้นได้ แทนการใช้ heap ในการเก็บข้อมูลค่ามากที่สุด

ทีนี้พอเวลาเจอหลายคำถาม ด้วยความที่จะหาคำตอบใหม่เรื่อยๆมันเสียเวลา เราจะเก็บคำถามทั้งหมดก่อน แล้วค่อย sort ไล่ตามจำนวนตาในการเล่น แล้วคำนวณไปเรื่อยๆพอจำนวนตาในการเดินเท่ากับคำถามไหน ก็จะตอบคำถามนั้น

ถ้าผู้เล่นเป็นคนที่ 1 (หมากขาว) ก็จะได้ว่าเอาค่า $dp[i][j]$ มาบวกได้ตรงๆ ในคำถามนั้นเลย
ถ้าผู้เล่นเป็นคนที่ 2 (หมากดำ) ก็จะได้ว่าทำแบบเดียวกัน แต่หาค่าเป็น $\min$ เป็นสมการ $dp$ แทนในคำถามนั้น

แต่ก็จะยังมีเคสดักเล็กน้อยคือ บางครั้งไม่ว่าเดินยังไงก็เดินไม่ถึงเส้นชัย บางครั้งอาจจะจงใจเดินให้ครบแบบไม่ถึงเส้นชัย บางครั้งเดินยังไงก็เลยเส้นชัย

ในเรื่อง memory สามารถลดจาก $N^2$ ช่องเหลือ $2N$ ช่องได้โดยการสลับมิติแรกให้เหลือ 2 เพื่อใช้สลับระหว่าง $dp[0]$ กับ $dp[1]$ ได้เพราะมีการใช้มิติก่อนหน้าแค่ 1 อาเรย์ (เนื่องจากก้าวไปแค่ทีละก้าว)

ส่วนพอได้คำคอบครบแล้ว ก็จะพิมพ์เรียงตามลำดับตามคำถามที่ได้มาตอนแรกเลย

หนีไปดวงจันทร์ (Moving to the Moon)

โจทย์ข้อ 7 หนีไปดวงจันทร์

https://github.com/Practical-Algorithm/Contests/blob/main/CodeAlgo2025/Code_Algo_2025-moving.pdf

ลองมาดูก่อนว่าการจะเลือกแบ่งของชิ้นเดียวนั้น ทำยังไงให้ดีที่สุด

สมมติมีของน้ำหนัก $p$ และแบ่งเป็น $q$ ส่วน (หลังจากนี้จะเรียกว่า $f(p,q)$ ) วิธีที่ดีที่สุดคือเราจะแบ่งทุกชิ้นให้น้ำหนักเท่ากันก่อน ( $\lfloor\frac{p}{q}\rfloor$ ) แล้วเอาเศษน้ำหนักที่เหลืออีก $p\bmod q$ หน่วย ไปกระจายใส่ให้ของที่เหลือให้กลายเป็น $\lfloor\frac{p}{q}\rfloor+1$ หน่วย ถ้าแบ่งวิธีอื่น cost ที่ได้จะไม่ได้ค่าน้อยที่สุด (ไปทดสอบเองได้)

ทีนี้จะได้ว่า cost ที่ได้จากการตัดแบ่ง คือ

f(p,q) = (q - (p\bmod q)) \times {\lfloor\frac{p}{q}\rfloor}^2 + (p\bmod q) \times {(\lfloor\frac{p}{q}\rfloor+1)}^2

สำหรับวิธีการแบ่งว่าเราควรแบ่งของแต่ละชิ้นกี่ครั้งดี จะเริ่มจากแบ่ง 0 ครั้งไปจนถึง $M$ ครั้ง และจะดูจากว่าในของทุกชิ้น อันไหนที่ค่า $f(p_i,\ q_i) - f(p_i,\ q_i+1)$ หรือ cost ที่ลดได้ มีค่ามากที่สุดเท่าที่ทำได้ โดยที่ $p_i,\ q_i$ คือน้ำหนักและจำนวนการตัดแบ่งของชิ้นที่ $i$ ขณะนั้น ซึ่งค่า cost ที่ลดได้ จะไม่มีทางเพิ่มขึ้นถ้าแบ่งต่อไปเรื่อยๆ (อีกแหละ ไปลองทดสอบเองได้)

ส่วนว่าจะใช้การแบ่งรวมทั้งหมดกี่ครั้งจะเทียบ cost ที่ลดได้จากการแบ่ง เอาไปเทียบกับ cost ที่เพิ่มจากการแบ่งเพิ่มอีก 1 ชิ้นแล้วดูว่ามันคุ้มไหมที่จะแบ่งต่อ ซึ่งก็สามารถใช้ Priority Queue เพื่อดูว่า cost ที่ลดได้ในการแบ่งที่ดีที่สุด ณ ตอนนี้เป็นเท่าไหร่ แล้วก็เทียบกับค่าใช้จ่ายในการแบ่งไปเรื่อยๆก็ได้

แต่ถ้าลองส่งไปดู จะเห็นได้ว่าการแบ่งยังมีประสิทธิภาพไม่เพียงพอ เราเลยจะใช้จุดที่บอกว่าค่า cost ที่ลดได้ จะไม่มีทางเพิ่มขึ้น

ทำให้สามารถใช้ binary search บนค่า cost ที่ลดได้ ( $x$ ) ****แล้วไป binary search ซ้ำอีกรอบบนของแต่ละชิ้นเพื่อหาว่าของแต่ละอันต้องแบ่งไปมากที่สุดกี่ครั้ง ( $y$ ) เพื่อให้ค่า cost ในการส่งที่ลดในการตัดครั้งถัดไป มันยังไม่น้อยไปกว่า $x$ หรือก็คือหาค่า $x$ และ $y$ ของของแต่ละชิ้นที่ $f(p_i,\ y) - f(p_i,\ y+1)$ ยังไม่น้อยกว่า $x$

ทีนี้เราจะเพิ่มหรือลดค่า $x$ ตอน Binary Search โดยดูจากเงื่อนไขว่า

ในการตัดแบ่งไปเนี่ย ทั้งหมดใช้รวมกี่ครั้ง ( $k$ ) โดยที่ต้องไม่มากกว่า $M$ เพราะโจทย์กำหนดว่าห้ามเกิน
cost ที่ลดได้ยังไม่น้อยกว่า cost ที่เพิ่มจากการแบ่ง $k$ ครั้งเพิ่มอีก 1 ครั้ง

ถ้าเข้าเงื่อนไขทั้งสองอัน แสดงว่าเราต้องแบ่งเพิ่มเพราะยังลด cost ได้อีกโดยลดค่า $x$ แต่ถ้าผิดเงื่อนไขสัก 1 ข้อหมายความว่าใช้การแบ่งมากเกินไป ทำให้ต้องลดการแบ่งลงมาโดยการเพิ่มค่า $x$

พอได้วิธีการตัดแบ่งที่ optimal สุดจากการ binary search ค่า $x$ แล้ว ก็เอาวิธีตัดแบ่งนั้นมาหาค่า cost ว่าเหลือเท่าไหร่ แล้วก็ตอบได้เลย

ขอบคุณที่ให้ความสนใจในการแข่งขัน code algo 2025 นะครับ

งานแข่งนี้เป็นการจัดขึ้นมาเป็นครั้งแรกของทีม ถ้าหากมีความเห็นหรือคำแนะนำเกี่ยวกับการแข่งขันในครั้งนี้สามารถบอกใน google form ด้านล่างนี้ได้เลยครับ
ขอบคุณครับ
ทีม Practical Algorithm

แบบประเมินหลังงาน CodeAlgo 2025

https://forms.gle/zYvit8qqynrhbau39

แชร์หน่อยก๊าบ ⊹

คัดลอกแล้ว!