Dynamic Programming คืออะไร? (Part 2)
ถึงรู้ว่า Dynamic Programming ต้องมี State แล้ว แต่การจะเขียนโปรแกรมจากการรู้แค่ State อย่างเดียวก็ยังไม่พอ บทความนี้จะอธิบายว่าจะเอา Recurrence Relation มาใช้ยังไงได้บ้าง


โพสต์นี้เป็นตอนที่สองของโพสต์ชุด Dynamic Programming ที่หลักๆจะอธิบายว่า Recurrence Relation คืออะไร และจะเขียนโปรแกรมจาก Recurrence Relation ได้ยังไง
ถ้ายังไม่ได้อ่าน Episode แรกของ Dynamic Programming แนะนำให้อ่านก่อนที่:
Dynamic Programming คืออะไร EP.1แล้วอะไรคือ Recurrence Relation?
จากตอนที่แล้วเรามีการกำหนดความหมายของแต่ละ state แล้ว step ถัดมาก็คือการเชื่อมโยงความเกี่ยวข้องของแต่ละ state ว่ามันเชื่อมกันด้วยสมการยังไง
Recap สักนิด
กลับมาที่ตัวอย่างเรื่องการทอนเหรียญ ก่อนหน้านี้เราได้สรุปไว้ว่า สิ่งที่เราต้องสนใจมีสองอย่าง
- ต้องทอนเงินเท่าไหร่
- มีเหรียญกี่ประเภท
(ในที่นี้เราสมมติว่ามีเหรียญแต่ละประเภท อย่างละไม่จำกัดด้วย)
เราก็เลยได้อาเรย์ DP หน้าตาแบบนี้มา:
โดย แทนจำนวนเงินที่ต้องทอน และ แทนว่าเราใช้เหรียญได้กี่ประเภท (ใช้ประเภทที่ ได้จนถึง ประเภท แต่ไม่ได้จำเป็นต้องใช้)
สมมติว่าเรามีเหรียญ บาท (สมมตินะ)
 รูปโชว์ตัวอย่างเหรียญ 5 และ 8 บาท
รูปโชว์ตัวอย่างเหรียญ 5 และ 8 บาท
 รูปโชว์ตัวอย่างเหรียญ 5 และ 8 บาท
รูปโชว์ตัวอย่างเหรียญ 5 และ 8 บาท
อย่างถ้า จะคิดซะว่าเราใช้ได้แค่เหรียญ บาท
 j=1 แปลว่าใช้เหรียญได้แค่เหรียญ 5
j=1 แปลว่าใช้เหรียญได้แค่เหรียญ 5
ถ้า ก็จะใช้เหรียญ หรือ ก็ได้
 j=1 แปลว่าใช้เหรียญได้ทั้งเหรียญ 5 และ 8 บาท
j=1 แปลว่าใช้เหรียญได้ทั้งเหรียญ 5 และ 8 บาท
ถ้างงว่าทำไมถึงกำหนดแบบนี้ แนะนำให้กลับไปอ่านโพสต์เรื่องการกำหนด state นะ(อยู่ต้นบทความ) โพสต์นั้นอธิบายละเอียดกว่านี้
แต่ถ้าเอาสั้นๆคือ
เราอยากได้คำถามที่ตรงกับสิ่งที่อยากจะหาคำตอบให้มากที่สุดแล้วสร้างเป็น state ขึ้นมาเพื่อเก็บคำตอบไว้
แล้วการกำหนดแบบนี้สำหรับโจทย์การทอนเหรียญก็จะช่วยให้เราหาคำตอบง่ายขึ้น
โยง state กัน
ต้องบอกก่อนว่า step นี้จะยาก หรือง่าย (หรือทำไม่ได้เลย) มันขึ้นอยู่กับว่าเราตั้งคำถามตอนสร้าง state ไว้ดีและครอบคลุมแค่ไหน ถ้ายิ่งตั้งให้ละเอียดก็ยิ่งโยงง่ายขึ้น แต่ก็แลกมากับการต้องให้โปรแกรมคิดเยอะขึ้นนะ
ก่อนที่จะสร้างสมการ Recurrence Relation เรามาลองคิดเป็นภาษาพูดกันก่อนว่ามัน make sense แค่ไหน
เช่น สมมติเรามีเหรียญสองประเภท บาท และ บาท
ถ้าเราไม่มีเหรียญสักแบบเลย ก็แปลว่าเราทอน บาทได้ นั่นแปลว่า
ซึ่งมันก็อาจจะฟังดูเหมือนไม่มีสาระอ่ะนะว่าคิดไปทำไม แต่มันจะมีประโยชน์ทีหลังเพราะต้องใช้เป็น base case
ถ้าเรารู้ว่าเรามีเหรียญ บาท(เหรียญประเภทที่ ) ก็แปลว่าเราทอนเงิน บาทได้
หรือจะบอกว่าเลือกที่จะไม่ใช้เหรียญ แล้วก็ไม่ทอนก็ทำได้เหมือนกัน (ทอน บาท)
อ่ะเอาใหม่ เรารู้ว่าสามารถทอน บาทได้ เราก็ใช้เหรียญ มาเพิ่มอีกเพื่อทอน บาทก็ได้
ถ้าเอามาเขียนเป็นสมการ จะได้ว่าเรากำลังถาม อยู่ ซึ่งแน่นอนว่าเราก็รู้ว่าเราทอน บาทได้ก็แปลว่า ดังนั้น
ซึ่งนี่ก็เหมือนเป็นการทอนเพิ่มไปอีก บาท โดยการใช้เหรียญ 5 บาท(ประเภทที่ 1)
คราวนี้ลองดูตัวอย่างที่ซับซ้อนขึ้นอีกนิด:
เรารู้อยู่แล้วว่าทอน บาทได้ แล้วทีนี้เรามีเหรียญ บาทด้วย(เหรียญประเภทที่ ) งั้นเราก็ทอน บาทได้ใช่มะ
รอบนี้เรากำลังถามว่า จะสามารถทอน บาทด้วยเหรียญ ประเภทได้ไหม state ก็เลยเป็น
งั้นเราก็ไปถามต่อว่า แล้วทอนเงิน บาทด้วยเหรียญที่มีได้ไหม
คำถามเลยกลายเป็นทอน บาทด้วยเหรียญ และ ได้ไหม และเราก็รู้อยู่แล้วว่าทำได้โดยใช้เหรียญ อย่างเดียวก็พอ ก็เลยได้ว่า
พอมาค่อยๆคิดตัวอย่างย่อยๆ เราจะได้ว่า
เมื่อ เป็นมูลค่าของเหรียญประเภท
ซึ่งแปลว่า การจะทอนเงินมูลค่า บาท ด้วยเหรียญ ประเภทได้ จะทำได้จากการลองทอนเหรียญมูลค่า ไปก่อนแล้วดูต่อว่าทำได้ไหม หรือ ทำได้อยู่แล้วโดยไม่ต้องใช้เหรียญประเภท เลย
ถ้าลองมองเป็นรูปภาพจะได้ว่า:
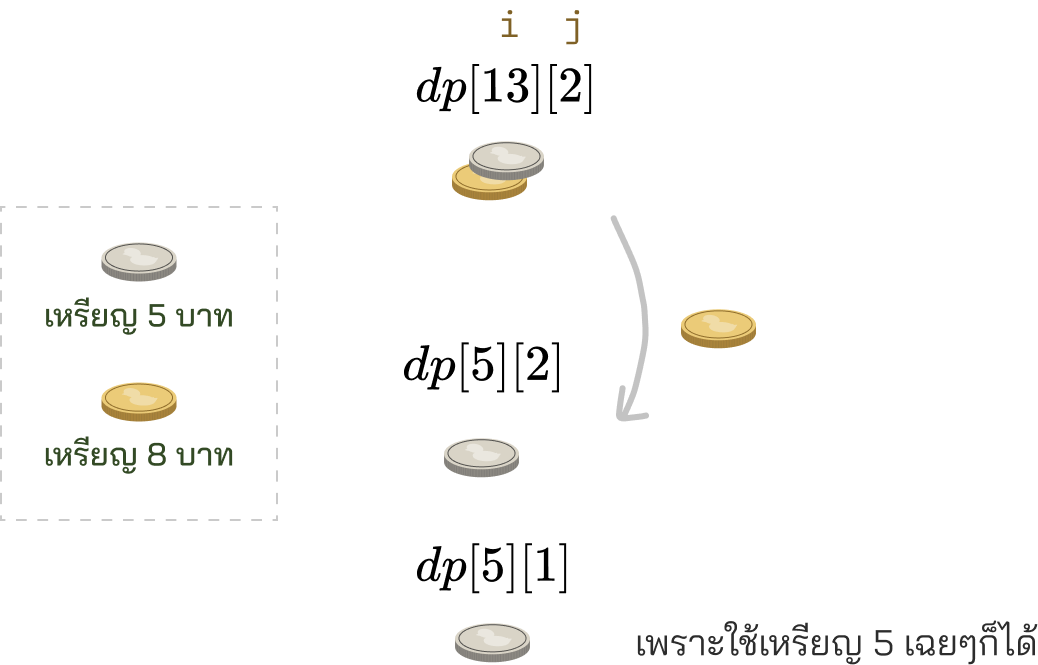 รูปความเชื่อมต่อของ state ที่เกี่ยวข้องกัน
รูปความเชื่อมต่อของ state ที่เกี่ยวข้องกัน
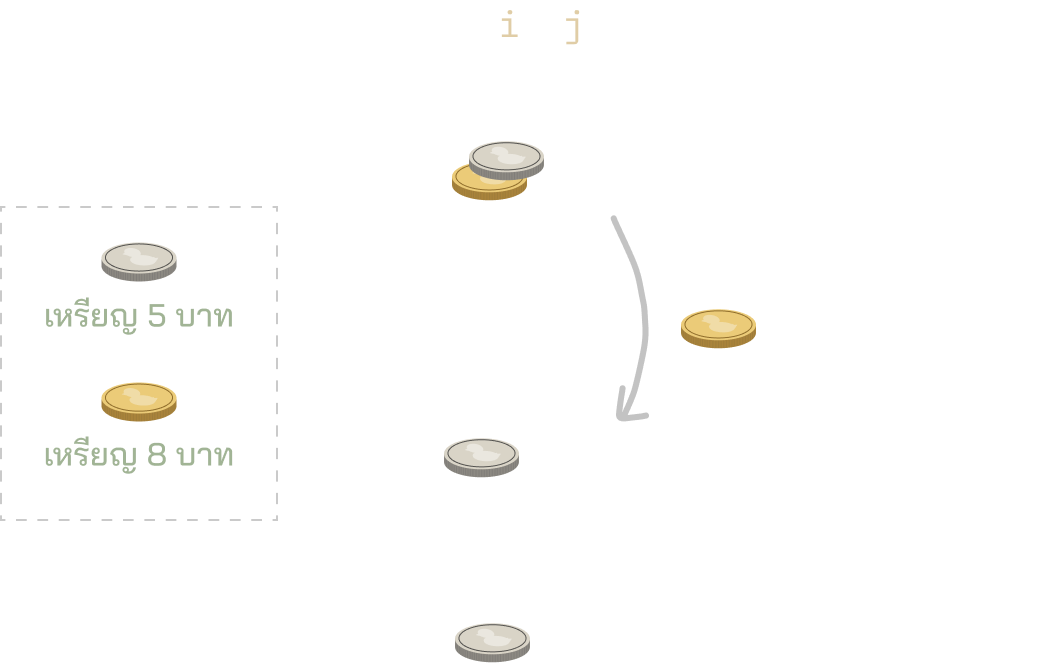 รูปความเชื่อมต่อของ state ที่เกี่ยวข้องกัน
รูปความเชื่อมต่อของ state ที่เกี่ยวข้องกัน
Tip: ถ้าลองเขียนตัวอย่างย่อยแล้วรู้สึกยังโยงความสัมพันธ์ยาก อาจจะต้องไปดูใหม่ว่าเรากำหนด state ละเอียดพอรึยัง
เขียนโปรแกรมจาก Recurrence Relation
จากตัวอย่างเรื่องการทอนเหรียญก่อนหน้านี้เราได้มาว่า
แต่ถึงได้มาแล้ว แล้วเอาไปทำไรอ่ะ จะไปเขียนโปรแกรมต่อยังไง?
การคำนวณ Recurrence Relation หรือจะหาค่าของแต่ละ state ทำได้อยู่ 2 แบบคือ
- คิดว่าค่า state ปัจจุบันมาจากอะไรได้บ้าง แล้วเอาค่าแต่ละส่วนมารวมกัน (Top-Down Approach)
- คิดว่าค่า state ปัจจุบันสามารถส่งผลถึง state อื่นๆไปยังไงได้บ้างแล้วส่งข้อมูลไปให้ (Bottom-Up Approach)
วิธีแบบ Top Down
วิธีนี้โดยส่วนตัวแล้วรู้สึกว่าเขียนง่ายว่าวิธี Bottom Up เยอะ เพราะว่าถ้าเราสังเกตดีๆ จาก Recurrence Relation ที่ได้มาตอนแรกเนี่ย มันก็เหมือนบอกกลายๆอยู่แล้วว่า เนี่ยมันจะได้ค่ามาจากอะไร
ก็ดูตามไปเลยว่า อ้อ เราต้องใช้ กับ ในการคำนวณ พอจะเขียนเป็นโค้ดเลยแปะมันตรงๆได้เลยว่า
1int dp(int i, int j){2 return dp(i, j - 1) | dp(i - v[j], j);3}ง่ายมะ เอาตรงๆก็เหมือนจะเขียนตาม Recurrence Relation แทบจะเป๊ะๆเลยด้วยซ้ำ
ทีนี้เราเหลืออยู่สองอย่างที่ต้องทำเพิ่มคือ
- เราไม่อยากคำนวณค่าเดิมซ้ำ
- โปรแกรมนี้มันรันไม่จบแน่ถ้าไม่มีเคสที่จะหยุดการ Recursive
เพิ่มการจำเข้าไป
การจำของ Dynamic Programming เขาจะเรียกว่า Memoization (ไม่ใช่ Memorization นะ) เพราะมันจำแบบ “ใช้เสร็จแล้วก็จบ โยนทิ้งได้” อะไรทำนองนั้น
ซึ่งวิธีจำเนี่ยก็ง่ายมากเลยคือ เราเห็นอยู่แล้วว่าโปรแกรมเราขึ้นอยู่กับค่า และ
1bool dp(int i, int j){2 return dp(i, j - 1) | dp(i - v[j], j);3}งั้นถ้าเราคำนวณ เสร็จแล้ว ก็แอบเอาไปเก็บไว้ที่ Array สักตัวนึงก็ได้ อย่างเช่น
แล้วถ้าโปรแกรมดันกลับมาถาม ใหม่อีกรอบ หลังจากที่เคยคำนวณแล้วรอบนึงก็ไม่ต้องคำนวณใหม่แล้ว ส่งค่า กลับไปให้เลยก็ได้ โค้ดใหม่ที่มีการจำเพิ่มก็จะกลายเป็น
1bool dp(int i, int j){2 if (dp_memo[i][j] is initialized) return dp_memo[i][j]; // ถ้าเคยคำนวณ dp_memo[i][j] ก็ตอบเลย3 return dp_memo[i][j] = dp(i, j - 1) | dp(i - v[j], j);4}แค่นี้ฟังก์ชัน นี้ก็จะไม่ต้องมาคำนวณซ้ำแล้ว เพราะเอาคำตอบมาจาก ได้เลย
แต่มันก็ยังไม่เสร็จ เพราะเรายังไม่ได้ทำเงื่อนไขหยุดการรันฟังก์ชันนี้เลย
Base Case เพื่อหยุด Recursion
ยังจำคำว่า Base Case จากตอนคิด Recurrence Relation ได้ไหม ที่ว่า
“ถ้าเราไม่มีเหรียญสักแบบเลย ก็แปลว่าเราทอน 0 บาทได้”
ที่ดูเหมือนจะไม่มีประโยชน์ในตอนนั้น ตอนนี้ถึงคราวได้ใช้แล้ว
การที่เราไม่มีเหรียญสักแบบเลยแปลว่า และการทอนเงิน 0 บาท ก็แปลว่า เมื่ออิงจากตัว สมการ Recurrence ที่ทดมาก่อนหน้านี้
ดังนั้นเราจะได้ว่า
ซึ่งมันแปลว่า ถ้าเราโดนถามว่า เราก็ตอบได้เลยเหมือนกันว่า ตอบ งั้นเพิ่มเงื่อนไขในฟังก์ชันเราต่อได้เป็น
1bool dp(int i, int j){2 if (i == 0 && j == 0) return true; // Base Case3 if (dp_memo[i][j] is initialized) return dp_memo[i][j];4 return dp_memo[i][j] = dp(i, j - 1) | dp(i - v[j], j);5}หมดรึยัง…? ยัง 555
นอกจากจะมี และ แล้ว มันยังมีอีกสำหรับการจะเขียน Top Down ถ้าลองคิดดีๆ แล้วตัวอื่นๆอย่าง ล่ะ จะให้ไปคำนวณตาม Recurrence Relation ก็ไม่ได้ เพราะ ก็กลายเป็นติดลบไปแล้ว (แปลว่าอะไร??) หรือ ก็ไม่มีอีกเพราะไม่มีของประเภทที่ 0 เนื่องจากนับจาก 1-index
เราก็เลยต้องมีเคสอื่นๆที่ว่า ถ้า แล้ว แต่ ก็ต้องตอบไปเลยว่าทำไม่ได้ หรือก็คือ นั่นแหละ
อีกอันนึงก็ถ้าอยู่ๆ มาถามว่าทอนเงินติดลบได้ไหม ก็คงไม่อ่ะเนอะ 😆 ดังนั้น ถ้า ก็ตอบ เหมือนกัน
สุดท้ายแล้วโค้ดก็จะออกมาหน้าตาประมาณนี้:
1bool dp(int i, int j){2 if (i == 0 && j == 0) return true;3 if (i < 0) return false; // Base Case ของการทอนเงินติดลบ4 if (j == 0) return false; // Base Case ของการทอนเงินแบบไม่มีเหรียญ5 if (dp_memo[i][j] is initialized) return dp_memo[i][j];6 return dp_memo[i][j] = dp(i, j - 1) | dp(i - v[j], j);7}โอเค เสร็จแล้ว จริงๆซะที เย่! 👍
จะเห็นว่าตัวโค้ดจริงๆแล้วคือเหมือนพยายามหาลงไปว่ามีวิธีไปหา Base Case ไหมนั่นแหละ
![dp[13][2] จะลงไปถามหา dp[13][1] และ dp[5][2] ลงไปเรื่อยๆ โดยในกรณีนี้จะผ่านไปทาง dp[5][2] ลงไปที่ dp[5][1] จนไปถึง dp[0][0] dp[13][2] จะลงไปถามหา dp[13][1] และ dp[5][2] ลงไปเรื่อยๆ โดยในกรณีนี้จะผ่านไปทาง dp[5][2] ลงไปที่ dp[5][1] จนไปถึง dp[0][0]](/images/082-dp-explained-2/fig5-light.png) การทำ Top Down ลงไปหา state 0,0
การทำ Top Down ลงไปหา state 0,0
![dp[13][2] จะลงไปถามหา dp[13][1] และ dp[5][2] ลงไปเรื่อยๆ โดยในกรณีนี้จะผ่านไปทาง dp[5][2] ลงไปที่ dp[5][1] จนไปถึง dp[0][0] dp[13][2] จะลงไปถามหา dp[13][1] และ dp[5][2] ลงไปเรื่อยๆ โดยในกรณีนี้จะผ่านไปทาง dp[5][2] ลงไปที่ dp[5][1] จนไปถึง dp[0][0]](/images/082-dp-explained-2/fig5-dark.png) การทำ Top Down ลงไปหา state 0,0
การทำ Top Down ลงไปหา state 0,0
วิธีแบบ Bottom Up
แทนที่จะคิดว่าค่าปัจจุบันมาจากไหนเหมือน Top Down จะเปลี่ยนใหม่เป็นคิดว่าค่าปัจจุบันสามารถส่งผลต่อช่องถัดๆ ไปยังไงได้บ้างแทน
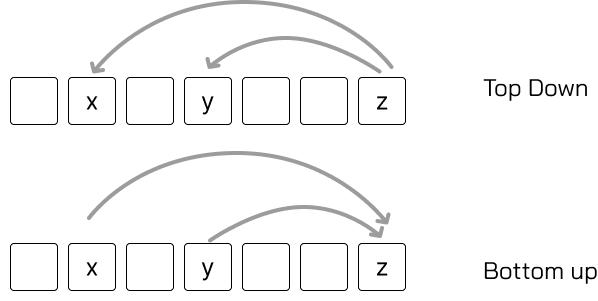 flow การวิ่งของข้อมูลเทียบระหว่าง Top Down กับ Bottom Up
flow การวิ่งของข้อมูลเทียบระหว่าง Top Down กับ Bottom Up
 flow การวิ่งของข้อมูลเทียบระหว่าง Top Down กับ Bottom Up
flow การวิ่งของข้อมูลเทียบระหว่าง Top Down กับ Bottom Up
มันจะลักษณะคล้ายๆ Top-Down เลยก็คือยังต้องการค่าจากช่องก่อนหน้าสักตัวนึงอยู่ดี ใช้ช่องเดียวกันนั่นแหละเพราะมันต้องทำตาม Recurrence Relation อ่ะนะ แค่แทนที่จะไปเรียกหาว่าค่าที่ต้องการเป็นอะไรเพื่อมาคำนวณ
ค่าในช่องเหล่านั้นต้องถูกคำนวณไว้ก่อนแล้วส่งคำตอบขึ้นมาหาช่องที่มันจะมีผลแทน อย่างในรูปเนี่ยถ้าเราคำนวณช่อง เสร็จ เราจะส่งข้อมูลบางอย่างไปหาช่อง เพื่อบอกว่า มันมีค่านี้ๆนะ เอาไปคิดต่อเอง เช่นเดียวกันคือ พอคำนวณค่า เสร็จ มันก็จะส่งไปบอกช่อง เหมือนกันว่า ค่า เป็นแบบนี้ๆ
แล้วพอเราไปถึงช่อง ก็แปลว่าเรารู้สิ่งที่ ช่อง ต้องการจะรู้ทั้งหมดแล้ว ก็คือเราได้คำตอบของช่อง แล้วนั่นแหละ
ซึ่งช่องที่เราจะเติมเนี่ยก็คือ Array นั่นแหละ
ส่วนที่ว่าจะต้องส่งข้อมูลให้ช่องไหนก็ดูได้จากตัว Recurrence Relation เหมือนเดิม (อีกแล้ว! 🫡)
จากตัวเดิมที่หน้าตาแบบนี้
เราจะต้องใช้ กับ ในการคำนวณใช่ไหม คิดกลับกันว่า ถ้าอย่างงั้น
กับ มีหน้าที่ที่จะต้องส่งข้อมูลให้ แทน
และถ้าเราเทียบเป็นว่า ต้องส่งข้อมูลให้ใครก็จะได้ว่าต้องส่งให้ กับ
หน้าตาตอนเขียน Bottom Up ก็เลยจะเริ่มมาแบบนี้
1for (int j=0;j<=w;j++){2 for (int i=0;i<=N;i++) {3 dp[i][j+1] |= dp[i][j]; // ส่งข้อมูลให้ dp[i][j+1]4 dp[i + v[j]][j] |= dp[i][j]; // ส่งข้อมูลให้ dp[i + v[j]][j]5 }6}แต่แน่นอนว่าแค่นี้มันก็ยังรันไม่ได้อ่ะนะ เรายังขาดไปอีกอย่างนึง คือ Base Case ที่เป็นตัวเริ่ม
Base Case ของ Bottom Up
อันนี้จะง่ายกว่าตอนทำแบบ Top Down หน่อย เพราะตอน Top Down เราต้องเตรียมกรณีให้ครบ ก็คือ
- กรณีทำได้ (เมื่อ และ )
- กรณีทำไม่ได้ (เมื่อ หรือ โดยที่ )
Bottom Up จะเอาแค่กรณีทำได้มาก็พอ แล้วให้ตั้งให้ที่เหลือใน เป็นทำไม่ได้ให้หมดเลย ก็คือแค่ตั้งให้ ก็พอแล้ว
ส่วนเรื่องการจำของ Bottom Up เนี่ย ตัวมันเองที่อัพเดท Array เรื่อยๆก็เป็นการจำไปในตัวอยู่แล้ว ดังนั้นเลยไม่ต้องเพิ่มอะไรมาช่วยจำอีก
แปลว่าโค้ดสุดท้ายตอนเขียน Dynamic Programming แบบ Bottom Up ก็จะได้ว่า
1dp[0][0] = true; // Base Case ของ Bottom Up2for (int j=0;j<=w;j++){3 for (int i=0;i<=N;i++) {4 dp[i][j+1] |= dp[i][j];5 dp[i + v[j]][j] |= dp[i][j];6 }7}ข้อสังเกต
ถ้าเรามองว่า Top Down คือเราจะพยายามลงไปหา state ที่เรารู้ว่าทำได้ Bottom Up จะเป็นการส่ง “การทำได้” ขึ้นไปจากตัวที่ทำได้อยู่แล้วขึ้นๆไป
สุดท้ายแล้วถ้าเขียนถูกตาม Recurrence Relation เดี๋ยวเราก็ได้ผลลัพธ์เดียวกันอยู่ดีไม่ว่าจะส่ง/รับข้อมูลยังไงอ่ะนะ
ข้อดีข้อเสีย
วิธีการแบบ Top Down มีข้อดีคือ
- ไม่ต้องหา state ทั้งหมดในทุกมิติก่อนหน้านั้น ทำให้เรียกใช้เท่าที่จำเป็น
- เรียกใช้ได้ค่อนข้างง่าย เพราะก็แค่จิ้มถามว่า ฟังก์ชัน เป็นอะไรเลย
ข้อเสียคือ
- เนื่องจากว่ามันเป็นฟังก์ชัน Recursive มันจะมี overhead cost หรือค่าในการเรียกตัวฟังก์ชันเอง เยอะกว่าการ access array ตรงๆ ของ Bottom Up
ส่วน Bottom Up Approach มีข้อดีคือ
- ตัวโค้ดทำความเข้าใจได้ง่ายกว่า เพราะมันไม่ใช่ Recursive
- การ access array ทำได้เร็วมาก ถ้าต้องการหาข้อมูลทั้งหมดของ นี้อยู่แล้ว จะไม่มีค่าเรียกฟังก์ชันแฝงมาด้วย
ข้อเสียคือ
- ต้องคำนวณหาค่า state ที่อยู่ก่อนหน้าทั้งหมดก่อน ถึงจะเอามาใช้คำนวณค่าของ state ปัจจุบันได้ ทั้งๆที่ส่วนใหญ่แล้ว หลายๆ state ที่คำนวณไปก็ไม่ได้มีประโยชน์ในการเอามาใช้เลย
ถ้ามีคำถามเพิ่มเติม มีเรื่องอื่นอยากให้มาเล่า หรืออยากติชมสามารถเข้ามาคอมเมนต์กันใน Facebook เรื่องเล่าชาวอัลกอ ได้เลยนะครับผม
Facebook เรื่องเล่าชาวอัลกอถ้าชอบโพสต์นี้ก็กดรูปหัวใจเพื่อเป็นกำลังใจให้ด้วยนะครับ แอดจะได้มีกำลังใจเขียนต่อไปเรื่อยๆ 😄


