Graph Theory มาจากไหน
Graph เป็นเนื้อหาส่วนนึงในเรื่อง Algorithms ที่เจอได้บ่อยมากทั้งในการเขียนโปรแกรมและการแก้ปัญหาในชีวิตประจำวัน โพสต์นี้เลยมาอธิบายที่มาคร่าวๆของทฤษฎีกราฟกัน


ในโพสต์นี้เราจะมาคุยกันเรื่อง ทฤษฎีกราฟ กันหน่อย ก่อนหน้านี้มีโจทย์หลายข้อละที่เป็นเรื่องกราฟก็เลยคิดว่าต้องเอามาอธิบายจริงๆจังๆละว่าทฤษฎีกราฟคืออะไรกันแน่
ก่อนอื่นเลยต้องเคลียร์กันก่อนว่ากราฟที่จะพูดถึงกันเนี่ย ไม่ใช่อันที่มันหน้าตาแบบนี้นะ
 รูปแผนภูมิเส้น
รูปแผนภูมิเส้น
ตัวนี้เรียกว่าแผนภูมิเส้น ไม่เกี่ยวกัน (พูดเรื่องนี้ทีไรโดนโยงไปหาแผนภูมิตลอด 😅)
ที่มาที่ไปของกราฟ
จริงๆแล้วด้วยความว่ากราฟ เป็นแค่คำย่อสั้นๆจากคำว่าทฤษฎีกราฟ ซึ่งมันเป็นแขนงนึงของวิชาเลข ที่มีความคาบเกี่ยวกันกับวิชาวิทยาการคอมพิวเตอร์
คือตอนแรกเลย วิชาเลขจะแทนหลายๆอย่างด้วยสมการ และสัญลักษณ์ (ซึ่งถ้าเราสังเกตดีๆ หลายๆแขนงของวิชาเลขมันก็ยังเป็นแบบนั้นอยู่อ่ะนะ) แต่พอเจอเรื่องความสัมพันธ์ระหว่างของหลายๆอย่าง จะเขียนเป็นสัญลักษณ์มันก็ยากละ
ที่มาของกราฟมันเกิดจากปัญหาเรื่อง Seven Bridges of Königsberg หรือ สะพานทั้งเจ็ดแห่งเมืองเคอนิชส์แบร์ค หลักๆของตัวปัญหานี้คือมีแผนที่ของเมือง Königsberg มาให้ที่ตัวเมืองนี้แบ่งได้เป็นพื้นดินอยู่ 4 ส่วน และพื้นดินเหล่านี้มีสะพานเชื่อมถึงกันอยู่ ตามรูป
 เมือง Königsberg ที่วาดใหม่
เมือง Königsberg ที่วาดใหม่
ชาวเมืองต้องการหาว่าถ้าจะเริ่มจากสักที่นึง แล้วเดินข้ามสะพานให้ครบทุกสะพานโดยที่ไม่ข้ามสะพานเดิมเลย จะทำได้ไหม จะเริ่มจากพื้นดินตรงไหนก็ได้ และจบตรงไหนก็ได้ แค่อยากเดินให้ครบทุกสะพาน
ซึ่งคนที่พยายามแก้ปัญหานี้ก็รู้แหละว่ามันทำไม่ได้ แต่ประเด็นคือก็พิสูจน์ไม่ได้เหมือนกันว่าทำไมมันทำไม่ได้ (ด้วยสมการ และสัญลักษณ์ที่มีอยู่ตอนนั้น)
นักคณิตศาสตร์ Leonhard Euler ที่พยายามพิสูจน์เรื่องนี้ออก เลือกที่จะวาดสัญลักษณ์นามธรรมตัวใหม่ขึ้นมาเรียกว่า โหนด (Node/Vertex) และ เส้นเชื่อม (Edge) เพื่อมาแทนเมือง และสะพาน ซึ่งกลายมาเป็นรากฐานของทฤษฎีกราฟอ่ะนะ
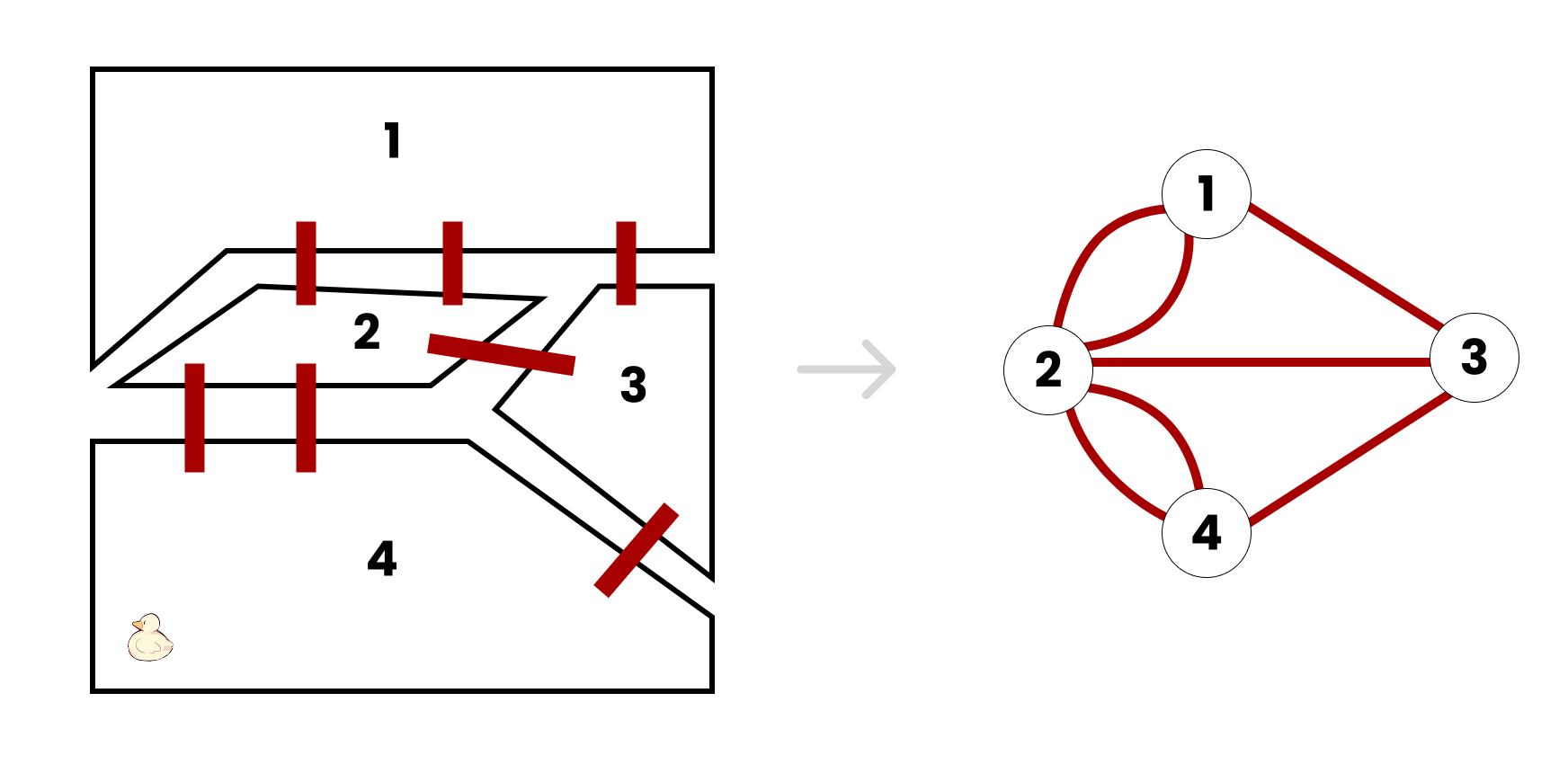 แปลงเมือง Königsberg เป็นกราฟ
แปลงเมือง Königsberg เป็นกราฟ
หลังจากวาดเป็นกราฟ ปัญหานี้ก็ได้ชื่อว่า Eulerian trail แทน และพิสูจน์ออกมาแล้วว่า “ต้องมี 0 หรือ 2 โหนดที่มี degree เป็นเลขคี่”
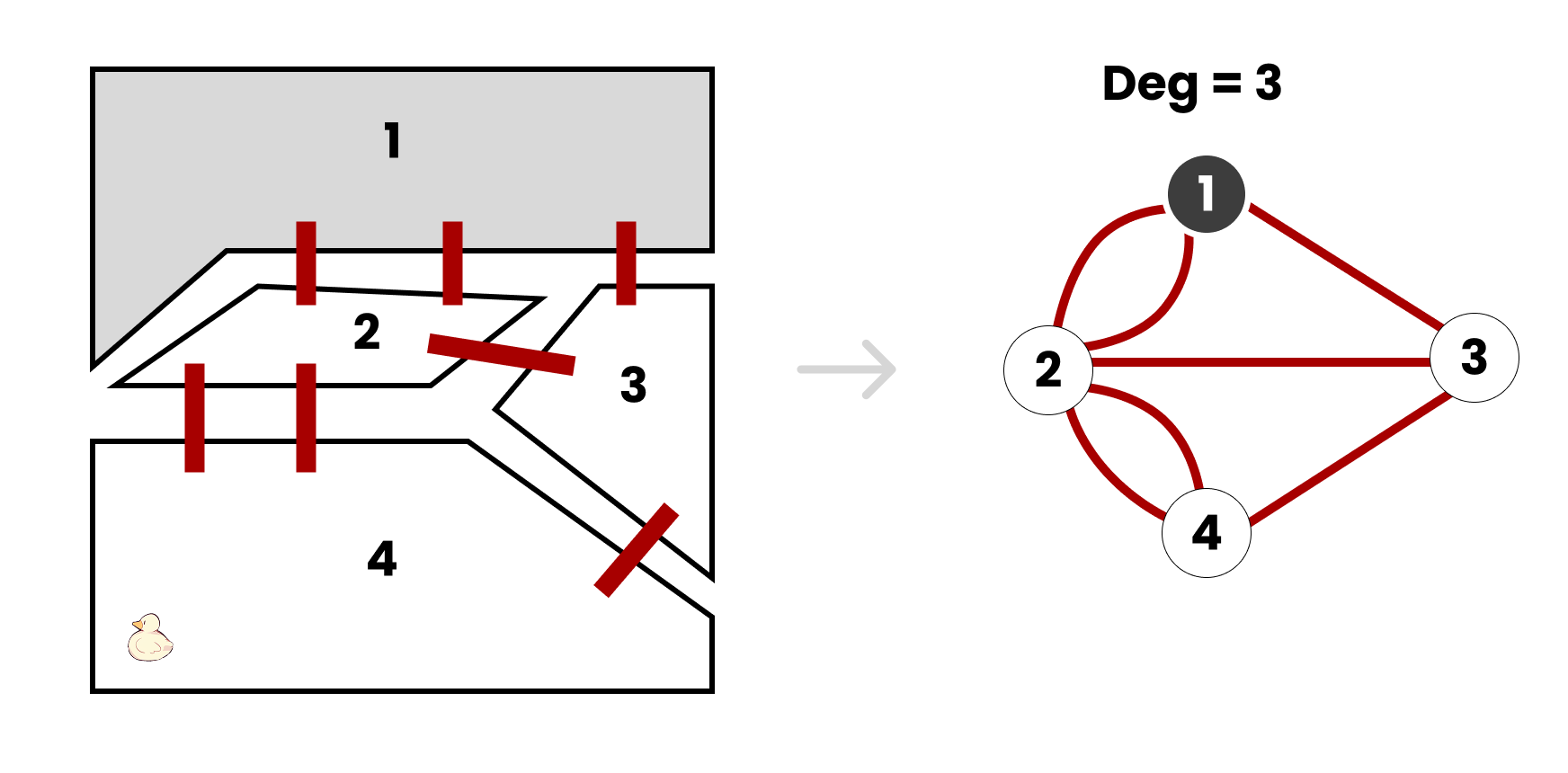 เมือง Königsberg ในรูปกราฟ ที่ highlight เมืองบนว่ามี deg 3
เมือง Königsberg ในรูปกราฟ ที่ highlight เมืองบนว่ามี deg 3
หลังจากที่มีการใช้กราฟกันมากขึ้น ปัญหารอบตัวหลายๆอย่างก็เริ่มถูกเอามาโมเดลใหม่ในรูปของ ความสัมพันธ์ระหว่างสิ่งของ ซึ่งหลักๆคือมันทำให้หลุดออกจากแค่สมการคณิตศาสตร์ แล้วมาอยู่ในรูปแบบที่มันมองเห็นและเข้าใจได้ง่ายขึ้น (โหนดกับเส้นเชื่อม)
แล้วรู้ไปทำไม
ถ้าเรามองดีๆแล้ว เกือบทุกอย่างที่อยู่รอบตัวเรามันโมเดลเป็นกราฟได้หมดเลย แล้วมันก็เอาไปใช้ได้เยอะมากเหมือนกัน
ถ้าเอาตัวอย่างที่ชัดเจนหน่อยก็พวกแผนที่ หรือแผนที่รถไฟฟ้า
 แผนที่รถไฟฟ้าในกรุงเทพ (แบบย่อ)
แผนที่รถไฟฟ้าในกรุงเทพ (แบบย่อ)
ที่เราสามารถแทนสถานีด้วย โหนด และสายรถไฟระหว่างสถานีด้วยเส้นเชื่อมก็ได้
หรือจะดูพวกการแข่งขัน tournament แบบแพ้คัดออกเหมือนอย่างของ Genwit ก็สามารถเอามมามองเป็นกราฟได้เหมือนกัน
แม้กระทั่งการเล่นเกมง่ายๆอย่าง XO ก็เอามาเขียนเป็นทฤษฎีกราฟได้นะ
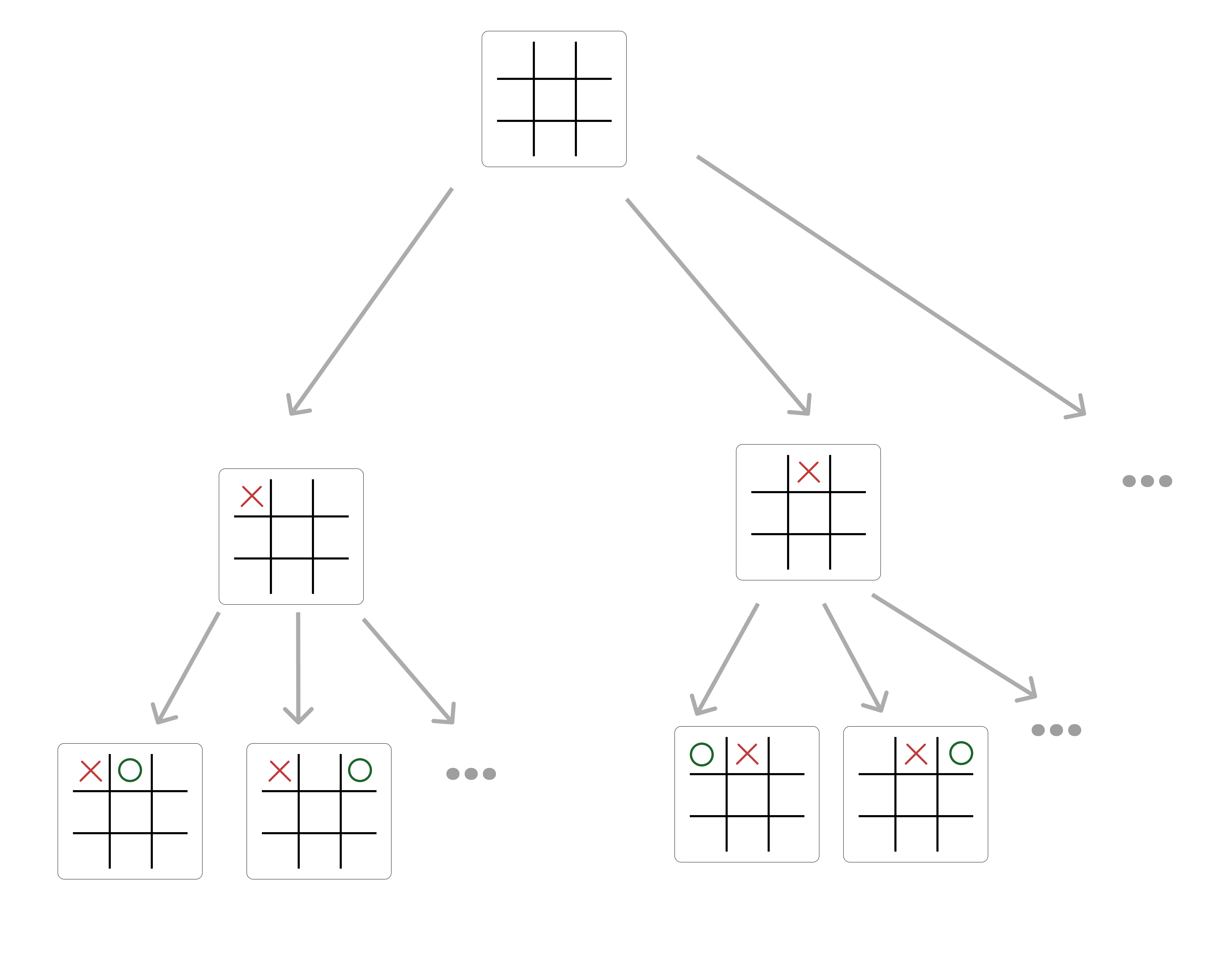 State Space Graph ของการเล่น XO
State Space Graph ของการเล่น XO
ซึ่งแบบนี้ก็จะใกล้เคียงกับที่เคยคุยเรื่อง เกม 24 ก่อนหน้านี้เหมือนกัน
กราฟลักษณะนี้จะเรียกว่า State-Space Graph ซึ่งเป็นกราฟที่เชื่อมความสัมพันธ์ระหว่างสถานะแต่ละสถานะที่สามารถเกิดขึ้นได้ในบริบทนั้นๆ
อ่านเกี่ยวกับเกม 24 และ State Space Graph ต่อได้ที่
เกม 24 กับ วิทยาการคอมพิวเตอร์พูดถึงบล๊อกก่อนหน้านี้ อันอื่นก็มีเหมือนกัน เช่น
เรื่องการระบายสีแผนที่ ที่สามารถเอามาเทียบกับการระบายสีบนกราฟได้:
โจทย์ระบายสีบนกระดาษพับ Origami ของ Genwit (Graph Coloring)หรือการทำ Syntax Highlight ที่สามารถใช้ Graph มาอธิบายความเชื่อมโยงระหว่างข้อมูลแต่ละส่วน
Code Editor ทำ Syntax highlight ยังไงเอาจริงๆแม้แต่การเขียน Dynamic Programming ก็ยังเป็นกราฟเลย
Dynamic Programming คืออะไร? (Part 1)แต่อันนั้นไว้เป็น Topic หลังจากนี้แล้วกัน ไว้คราวหน้าจะมาอธิบายเพิ่มว่ากราฟมันมีลักษณะไหนได้บ้างนะฮะ


