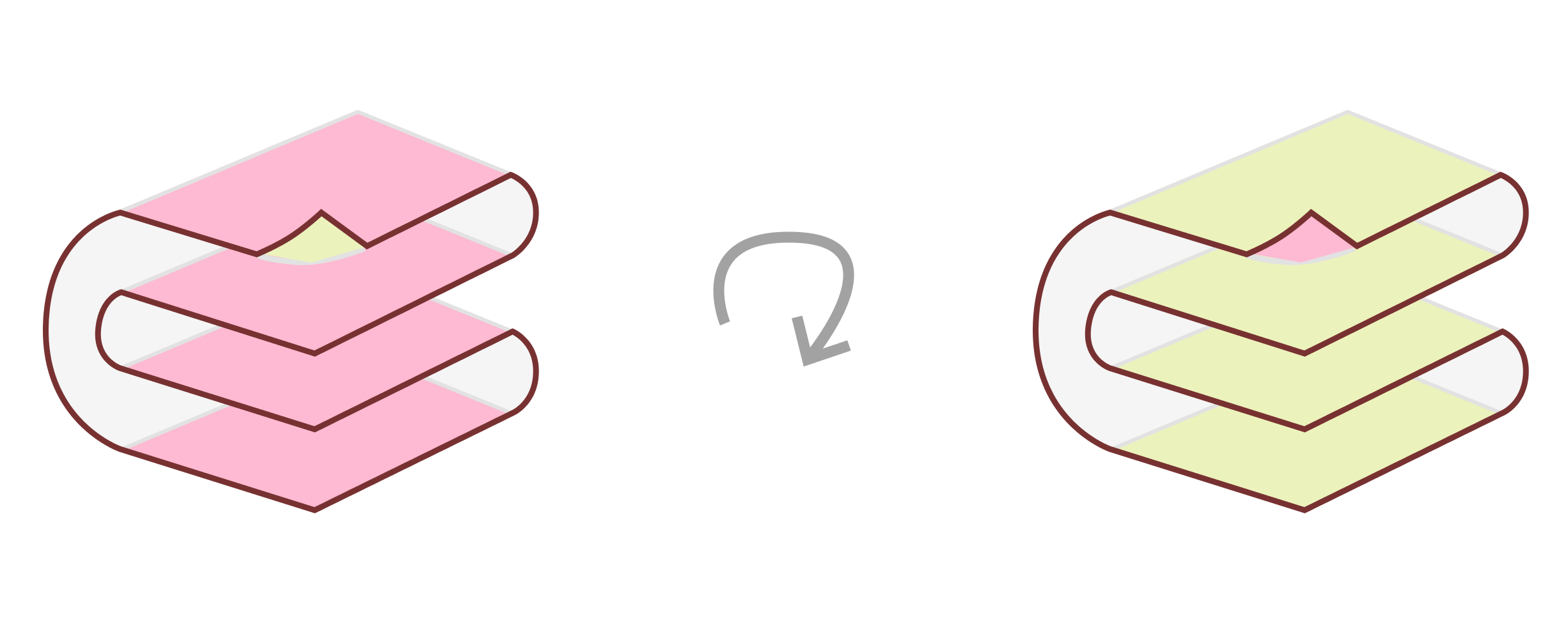Practical Algorithmsโจทย์ระบายสีบนกระดาษพับ Origami ของ Genwit (Graph Coloring)
ถ้าใครไม่เห็นโจทย์ใน GenWit หรือยังไม่ได้ดู แวบไปดูก่อนได้ฮะ รอบนี้สนุกดี
Genwit อัจฉริยะพันธุ์ใหม่ EP. 13หรือจะดูจากรูปโจทย์ด้านล่างก็ได้
โจทย์ Genwit EP.13
ถามว่าถ้าเราพับกระดาษ Origami แบบนี้แล้วจะใช้สีในการระบายหน้ากระดาษอย่างน้อยสุดกี่สีถึงจะพอ เพื่อให้แต่ละหน้าที่ติดกันไม่ใช่สีเดียวกัน
Graph Coloring คืออะไร?
ขอเท้าความสักเล็กน้อยว่านี่เป็นโจทย์แบบนึงในวิชาวิทยาการคอมพิวเตอร์อยู่แล้วที่ชื่อว่า Graph Coloring โดยเราจะได้กราฟ(แบบคอมพิวเตอร์) มาอันนึงแล้วถามว่าต้องระบายสีโหนด (วงกลม) ยังไงเพื่อให้วงกลมที่มีเส้นเชื่อมติดกันเป็นคนละสี และใช้จำนวนสีที่ต่างกันให้น้อยที่สุดเท่าที่จะเป็นไปได้
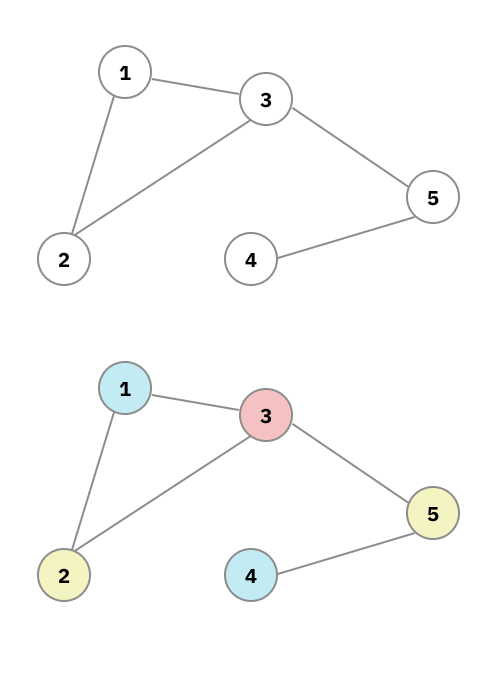การทำ Graph Coloring
ซึ่งโจทย์ข้อนี้ของ Genwit ก็คือการทำ Coloring เลยนั่นแหละ เพราะถ้าเราเทียบให้ หน้า(Face) ของตัวกระดาษเป็นโหนด แล้วให้หน้าที่ติดกันที่โดนคั่นด้วยรอบพับ เชื่อมกัน เราก็จะได้เป็นกราฟออกมาเลย
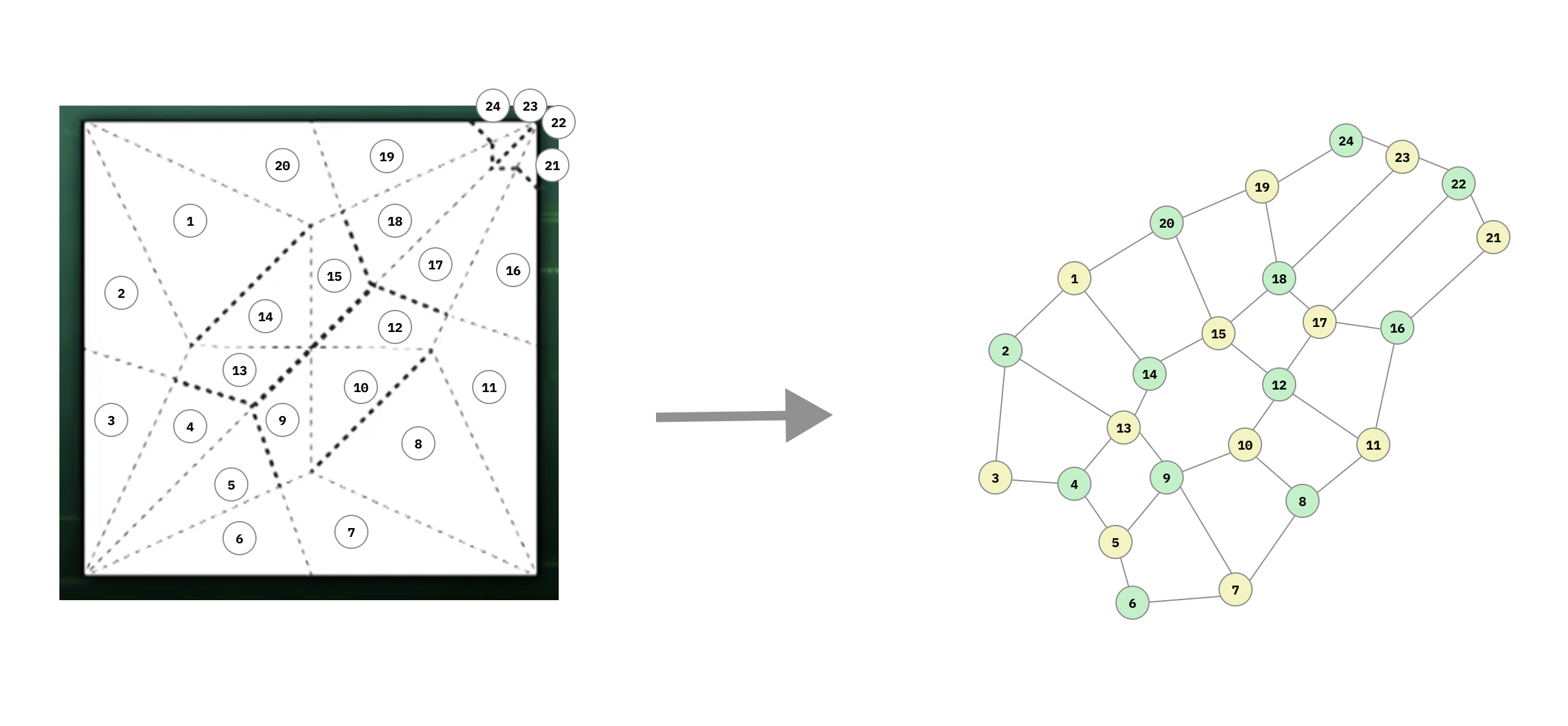แปลงโจทย์กลายเป็นกราฟ
ซึ่งก็จะเห็นว่าถ้าเราพับกระดาษแบบในโจทย์ เราจะได้กราฟที่มีหน้าตาแบบนี้ที่เราระบายสีได้ด้วย 2 สีเลย แต่เดี๋ยวจะอธิบายเพิ่มว่าทำไม 2 สีได้ตลอด
Planar Graph กับ 4-color Theorem
ทีนี้พอเรามองเป็น Graph Theory เนี่ย กราฟบางตัวมันจะมีคุณสมบัติพิเศษเรียกว่า Planar Graph โดยคุณสมบัตินี้มันหมายความว่าเราสามารถวาดกราฟให้เส้นเชื่อมทุกเส้นไม่ตัดกันเองเลยได้
ตัวอย่างกราฟที่ไม่เป็น Planar:
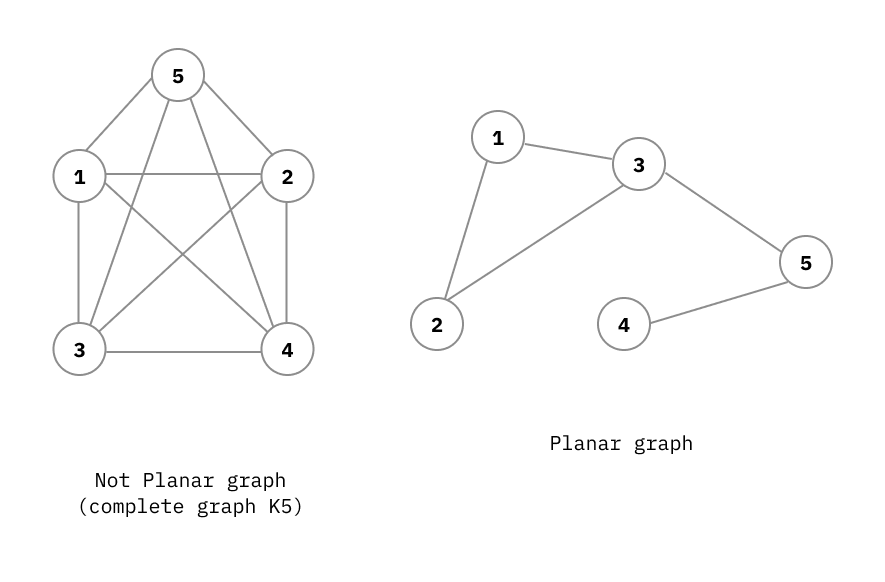Complete Graph ขนาด 5 หรือเรียกว่า K5 ก็ได้
เพราะกราฟแบบนี้มันไม่สามารถวาดให้เส้นเชื่อมมันให้ไม่ตัดกันได้ ก็เลยไม่เป็น Planar Graph
ซึ่งจากรูปข้างบนของโจทย์ Genwit เส้นเชื่อมมันไม่ได้ตัดกัน โจทย์นี้ก็เลยเหมือนว่าถามว่า Planar Graph นี้ใช้กี่สีระบายนั่นแหละ
ทีนี้มันเป็น Planar Graph แล้วยังไง คือมันจะมีทฤษฎีอยู่ตัวนึงชื่อว่า 4-color Theorem ที่ถ้าเอาอย่างย่อๆ จะบอกว่ากราฟไหนก็ตามที่สามารถวาดให้เป็น Planar Graph ได้ จะสามารถระบายได้โดยใช้สีไม่เกิน 4 สี
ดูตัวอย่างแผนที่เมกาก็ได้เหมือนกัน:
ถามว่ามีพิสูจน์ไหม ก็มีแหละ แต่เขียนไม่ไหวเยอะเกิน ดูตัวที่สำคัญกับโจทย์ตอนนี้ดีกว่า 555
เพราะมันมีทฤษฎีอีกตัวชื่อว่า Grötzsch’s theorem (แอดอ่านไม่ออก 🤣) ที่บอกไว้ว่า ถ้าใน Planar Graph ที่ว่าเนี่ยไม่มีสามเหลี่ยมในนั้นเลย กราฟนั้นสามารถระบายได้ด้วย 3 สีแทนที่จะเป็น 4 สี
สามเหลี่ยมที่ว่าคือ
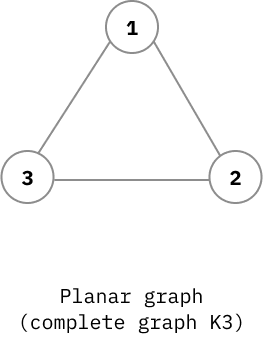กราฟสามเหลี่ยม K3
ซึ่งถ้าสังเกตดีๆตัวโจทย์การพับกระดาษก็เข้าเงื่อนไขนี้เหมือนกัน แต่ถ้าดู Genwit จบแล้วจะเห็นว่าคำตอบมันไม่ใช่ 3 หนะสิ
สาเหตุคือการพับกระดาษ Origami เนี่ยมันมีคุณสมบัติเฉพาะตัวอีกเหมือนกัน นอกจากว่ามันจะเป็น Planar Graph ที่ไม่มีสามเหลี่ยมแล้ว ตรงรอยตัดของเส้นพับบนกระดาษเนี่ยจะเชื่อมอยู่กับหน้ากระดาษเป็นเลขคู่เท่านั้น (จากทฤษฎีการพับกระดาษของ Maekawa)
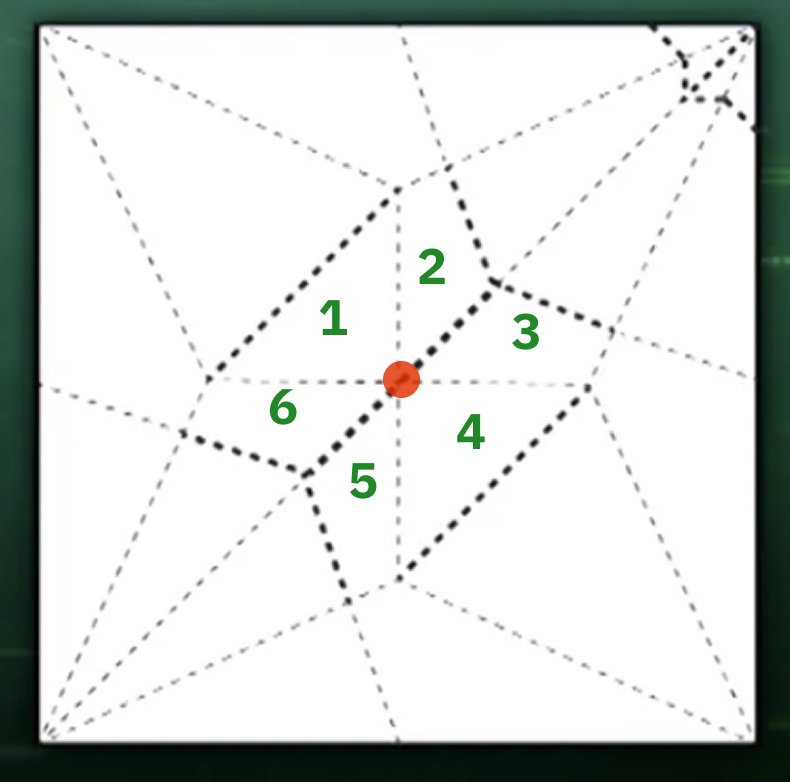นับจำนวนหน้ารอบๆจุดตัด
แล้วการที่มันเป็นแบบนี้ทำให้ตอนที่เราแปลงเป็นตัวกราฟจะไม่มี cycle ที่มีความยาวเป็นเลขคี่
ซึ่งการที่ไม่มี Cycle ที่มีความยาวคี่เลย ก็จะเหมือนกับว่ากราฟรบอรอยตัดอันนั้นที่ได้จะหน้าตาแบบนี้:
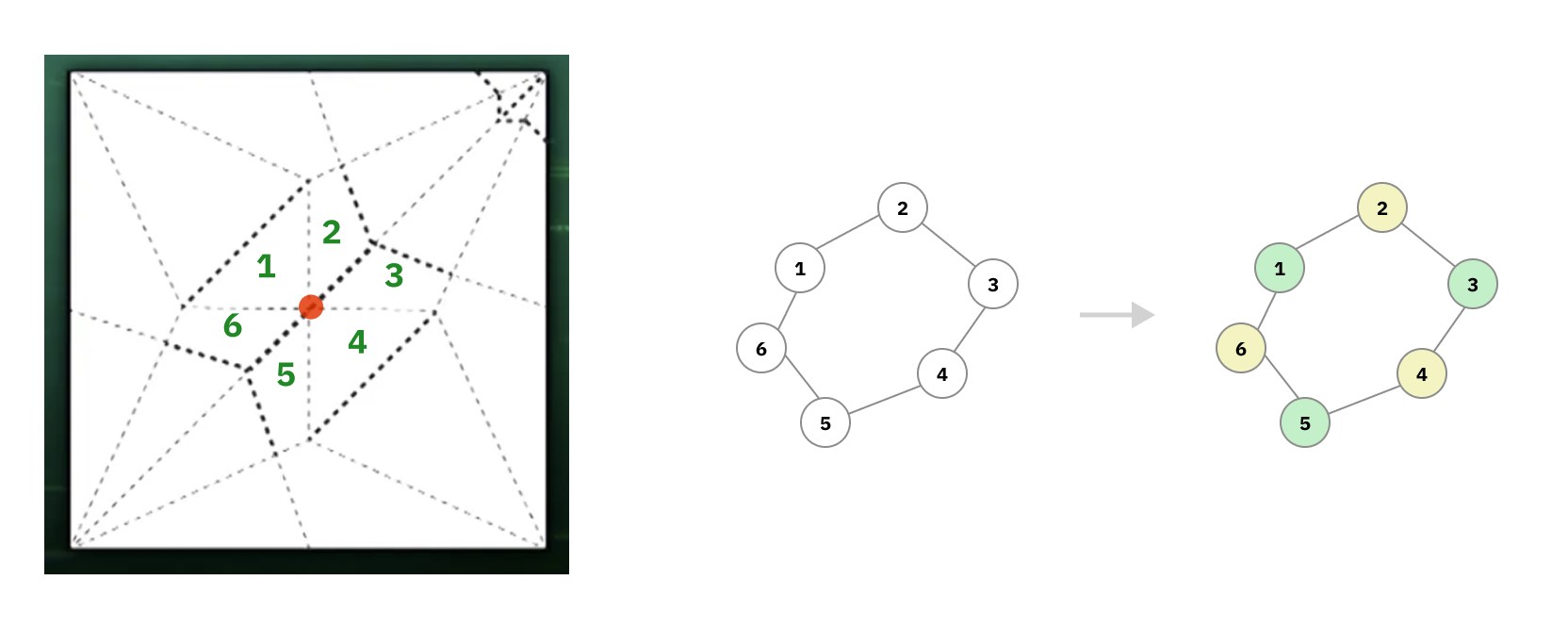
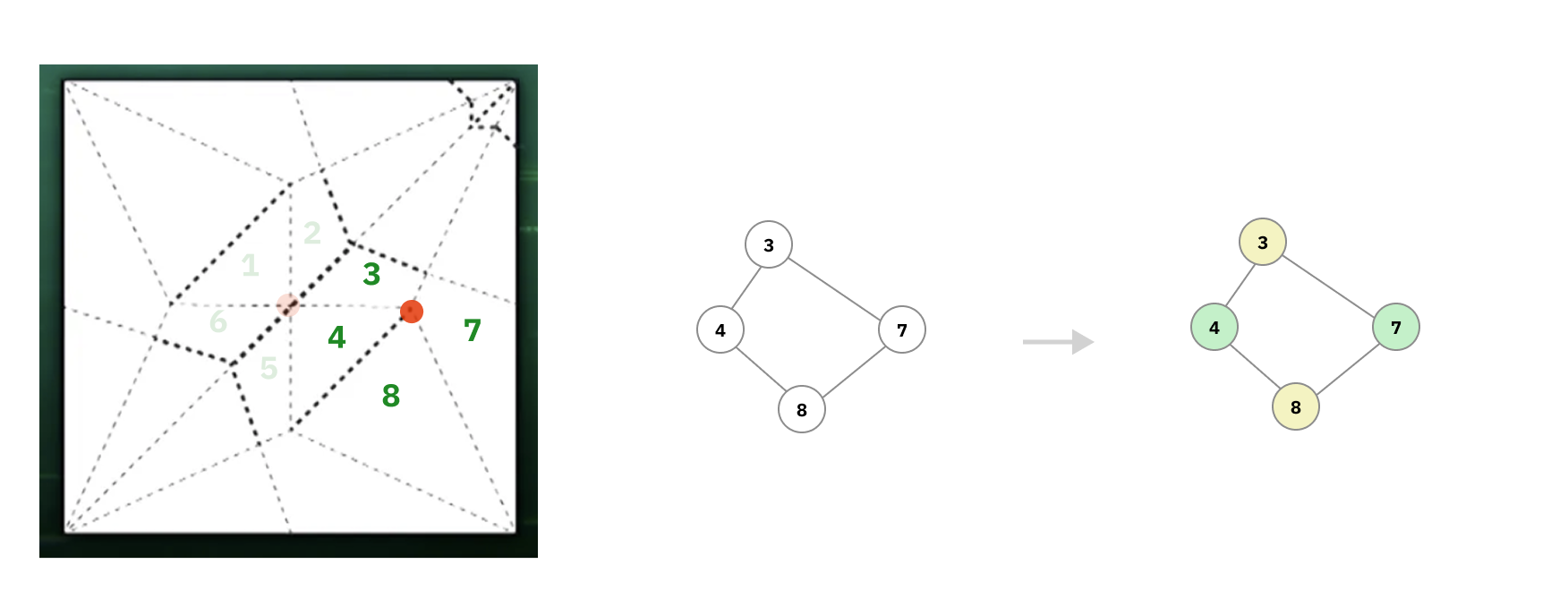การแปลงรอบจุดตัดให้เป็นกราฟ
ที่เราสามารถแบ่งระบายสีออกเป็นสองฝั่งได้แบบนี้ ที่ในทางคอมพิวเตอร์จะเรียกว่า Bipartite Graph ทีนี้คืออันนั้นมันรอบจุดตัดจุดเดียวไง แต่ในการพับกระดาษมันมีหลายจุดตัดระหว่างรอบพับใช่มะ เราเลยต้องมาดูว่าแต่ละจุดตัดมันสัมพันธ์กันยังไงด้วย
ถ้าเรามองสองจุดตัดที่อยู่ติดๆกัน เราจะสามารถลากเส้นตามรอยพับได้แบบนี้
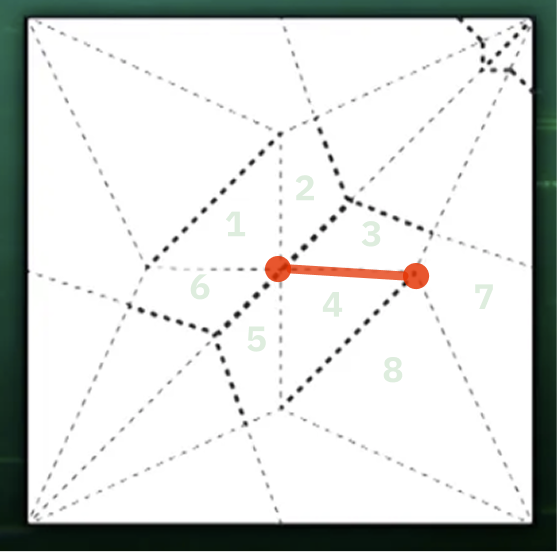เส้นรอยพับกระดาษที่เชื่อมจุดตัดสองจุดเข้าด้วยกัน
ซึ่งทุกรอยพับที่ว่าเนี่ย ยังไงมันก็ต้องคั่นระหว่างหน้า 2 หน้าใช่ไหมล่ะ (ไม่งั้นมันก็ไม่ใช่รอยพับ) ดังนั้นพอเราจะเอากราฟที่ได้จากทั้งสองจุดมาเชื่อมกัน เราก็เชื่อมเข้ากับแค่ 2 จุดที่มันโดนคั่นด้วยรอยพับนั้นก็พอ
แล้วมันก็จะได้หน้าตาแบบนี้
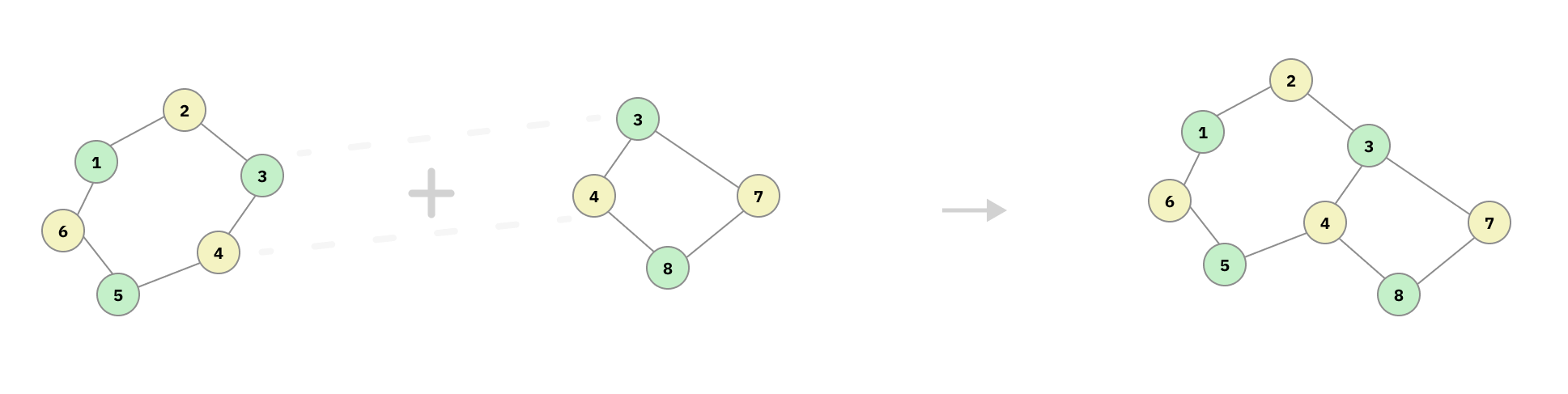cycle 2 อันมาเชื่อมกัน
ซึ่งสังเกตว่าถึงตอนเชื่อมสีจะไม่เหมือนกัน เราก็สามารถสลับสีเพื่อให้มันกลับมาเหมือนกันก่อนแล้วค่อยเชื่อมก็ได้ มันไม่ได้ผิดอะไร แล้วก็ด้วยความที่มันจะไม่มี Cycle ขนาดคี่ยังไงกราฟพวกนี้ก็ต่อกันได้
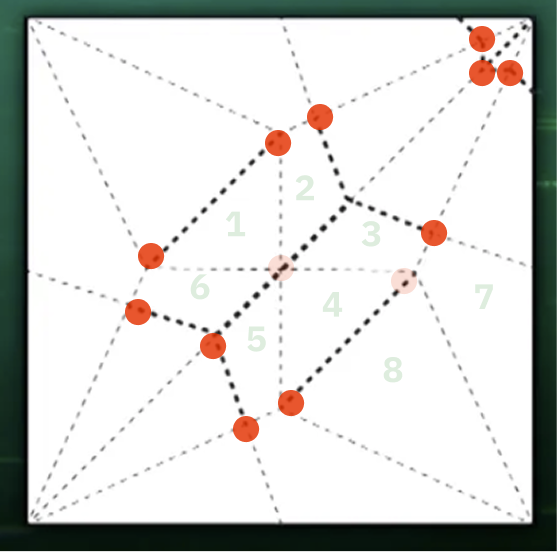จุดตัดที่เหลือที่ต้องไปเชื่อมอีก
และหลังจากนั้นเราก็แค่เชื่อมแบบนี้ไปเรื่อยๆมันก็จะครบทั้งกราฟเอง และก็ยังใช้แค่ 2 สีเหมือนเดิมเพราะยังไงเราก็ยังสลับสีตัวที่ต้องเข้ามาต่อให้มันตรงกับตัวที่มีอยู่ก่อนหน้าได้อยู่ดี
ซึ่งแปลว่าต่อให้พับกระดาษยังไง(ไม่จำเป็นว่าเป็นแค่รูปนก) ขอแค่กระดาษไม่โดนตัดหรือฉีก มันก็ระบายด้วย 2 สีได้ตลอดอยู่ดี
วิธีอื่นๆ
มองภาพกระดาษเป็นเหมือนการพับทบก็ได้ เพราะถ้ามองว่ากระดาษสามารถถูกพับให้มันแบนได้ เราก็มองว่าด้านที่หันขึ้นข้างบนเป็นสีนึง และด้านที่หันลงด้านล่างเป็นอีกสีนึงก็ได้เหมือนกัน เพราะการที่จะเปลี่ยนจากด้านบนไปด้านล่างมันก็ต้องผ่านรอยพับ ซึ่งก็เหมือนกับการทำ Coloring อยู่ดี เพราะมันเชื่อมกันด้วยเส้นเชื่อม(รอบพับ)
อ้างอิง
The Math for Folding Origami
https://naturalorigami.wordpress.com/2016/06/27/the-maekawa-theorem/
