วิเคราะห์โจทย์ TOI13 ข้อ Timerswitch
โจทย์
เราต้องการทำ operation การหมุนคือเอาตัวอักษรหน้าสุดไปต่อท้ายสตริง เช่น 001001 เป็น 010010 บนสตริงเริ่มต้นที่โจทย์ให้มา
โดยสตริงเริ่มต้นที่ว่ามีความยาว และประกอบด้วยเลข 0 หรือ 1 เท่านั้น
โจทย์อยากรู้ว่าต้องทำ operation หมุนนี้อย่างน้อยกี่ครั้ง ถ้าโดนบังคับทำอย่างน้อย 1 ครั้ง ถึงจะหมุนกลับมาได้สตริงเหมือนสตริงเดิมที่ให้มาในข้อมูลนำเข้า
ข้อมูลนำเข้า
บรรทัดที่ 1 จำนวนเต็มบวกหนึ่งจำนวน คือ ระบุขนาดของสตริง โดยที่
บรรทัดที่ 2 สตริงขนาด ที่ประกอบด้วย 0 และ 1
ข้อมูลส่งออก
มี 1 บรรทัด แสดงจำนวน operation การหมุนที่น้อยที่สุด โดยที่ต้องทำอย่างน้อย 1 ครั้งเพื่อให้กลับมาเป็นสตริงตั้งต้น
ตัวอย่างข้อมูลนำเข้าและข้อมูลส่งออก
| Input | Output |
|---|---|
| 10 1010101010 | 2 |
| 10 1000000010 | 10 |
| 5 00000 | 1 |
| 5 10000 | 5 |
คำอธิบายตัวอย่างแรก:
ถ้าทำการหมุน 1 ครั้งจะได้เป็น 0101010101
ถ้าทำการหมุน 2 ครั้งจะได้เป็น 1010101010 ซึ่งเป็นสตริงเดียวกับที่ให้มาใน input
วิเคราะห์โจทย์
ก่อนอื่น เรามาดูวิธีที่หาคำตอบได้ชัวร์ๆ ก่อน เพื่อให้รู้ว่าเราควรจัดการยังไงกับปัญหานี้
เริ่มแรก โจทย์มันอยากรู้ว่าต้องหมุนกี่รอบมันถึงจะเหมือนเดิม ดังนั้นวิธีแรกที่พอทำได้แน่ๆ ก็คือหมุนสตริงมันไป รอบไปเลย เพราะเมื่อหมุน รอบ ยังไงมันก็กลับมาเหมือนเดิมแน่ๆ
แต่โจทย์ก็คงไม่ได้อยากให้ตอบ ตลอดอ่ะเนอะ ไม่งั้นจะทำไปทำไม 😆
ดังนั้นเราก็สรุปคร่าวๆพอได้ว่า มันน่าจะต้องมีสตริงสักอันนึงก่อนที่จะหมุนครบ รอบที่มันเหมือนบ้างแหละ ซึ่งเราก็สามารถเอาสตริงเหล่านั้นมาเช็กแต่ละตัวเลยว่าอันไหนที่ตรงกับสตริงเริ่มต้นบ้างก็น่าจะได้
เปรียบเทียบสตริงระหว่างการหมุน
ลองดูตัวอย่างสตริง 001001 ถ้าเอามาหมุน ครั้ง จะได้สตริงแต่ละแบบตามลำดับด้านล่าง
-
010010
-
100100
-
001001
-
010010
-
100100
-
001001
ในตัวอย่างนี้จะเห็นว่าเราไม่จำเป็นต้องหมุนครบ ก็มีสตริงที่วนกลับมาเหมือนเดิมแล้ว ทำให้เราต้องไล่เทียบ สตริงที่เกิดจากการหมุนในแต่ละขั้น เพื่อดูว่าแต่ละตำแหน่งว่าตรงกันทั้งหมดมั้ย
โดยในส่วนของการเทียบสตริงกันระหว่าง 2 สตริงเนี่ย วิธีง่ายสุดคือแบบเทียบทีละตัวอักษรไปเลย ซึ่งแปลว่าเราต้องเทียบไป ตัวอักษรทุกครั้งที่จะเทียบสองสตริง
ไม่พอเราต้องเทียบทั้งหมด คู่ เพราะต้องเทียบทุกสตริงที่หมุนมาได้กับสตริงเริ่มต้น ซึ่งมีทั้งหมด สตริง ทำให้สุดท้ายแล้วเราต้องเทียบตัวอักษรทั้งหมด ครั้งในเคสแย่ที่สุด ซึ่งยังทำไม่ทันในเวลาที่โจทย์กำหนด เพราะประสิทธิภาพยังไม่ดีพอ (ค่า มันเยอะเกินไปที่จะทำแบบนี้ได้)
ทีนี้เราก็เลยต้องหาทางลดเวลาในการเทียบแต่ละสตริงที่หมุนมาได้ ซึ่งหนึ่งในวิธีที่ทำได้คือการ Hashing หรือก็คือการแปลงสตริงเป็นเลขซักค่านึง เพื่อให้เทียบค่าว่าสตริงเหมือนกันมั้ยด้วยเวลาที่เร็วขึ้น เนื่องจากการเทียบตัวเลขตัวเดียวมันเร็วกว่าการเทียบทีละตัวอักษรเยอะ
ขั้นตอนการทำ Hashing
ในการทำ Hashing หรือการแปลงสตริงเป็นเลขเนี่ยเราจะเรียกผลลัพธ์ที่ได้ว่า เมื่อ คือสตริงใดๆที่เราส่งไป Hash
สมมติด้วยตัวอย่างก่อนโดย เราจะใช้หลักการของเลขฐาน 2 เพื่อ Hash
โดยเราสามารถแปลง 001001 เป็นค่า Hash ได้ดังตารางด้านล่าง
| String | 0 | 0 | 1 | 0 | 0 | 1 |
|---|---|---|---|---|---|---|
| Value |
ในกรณีนี้เราให้ตัวเลขที่อยู่ซ้ายสุดของสตริงมีค่าตัวคูณมาก และขวาสุดคูณน้อย แล้วเอาค่า หรือ ที่อยู่บนสตริงเป็นตัวคูณ เราจะได้ว่า
เลื่อนสตริงที่จะแปลงเรื่อยๆ
ทีนี้เราจะใช้ข้อสังเกตว่าการทำ operation หมุน ทำให้สตริงที่ได้มาจะเป็นสตริงที่เลื่อนไป 1 ตำแหน่งจากอันก่อนหน้าตลอด
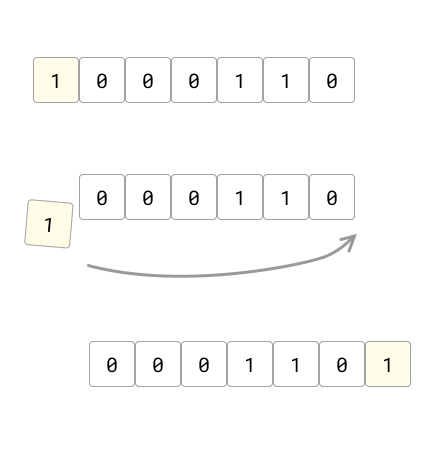 รูปแสดงสตริงใหม่ที่ได้จากการหมุน
รูปแสดงสตริงใหม่ที่ได้จากการหมุน
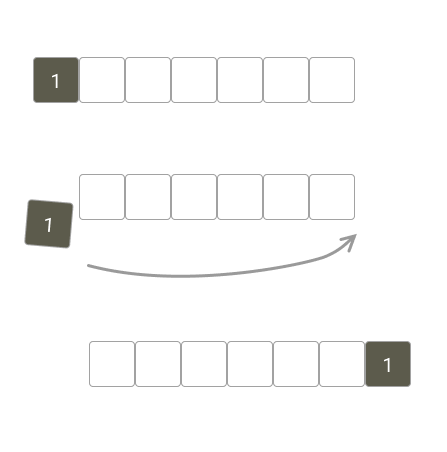 รูปแสดงสตริงใหม่ที่ได้จากการหมุน
รูปแสดงสตริงใหม่ที่ได้จากการหมุน
ทำให้เรารู้ว่าจะมีตัวถูกเปลี่ยนแค่ 2 ตัวคือตัวที่อยู่ทางซ้ายสุดที่จะหายไป และจะมีตัวมาต่อท้ายทางขวาสุด จึงทำให้สามารถลดเวลาหาค่า อันใหม่ได้โดย
- คูณค่า Hash ไป 2 เพื่อเปรียบเสมือนเลื่อนสตริงไปทั้งซ้าย
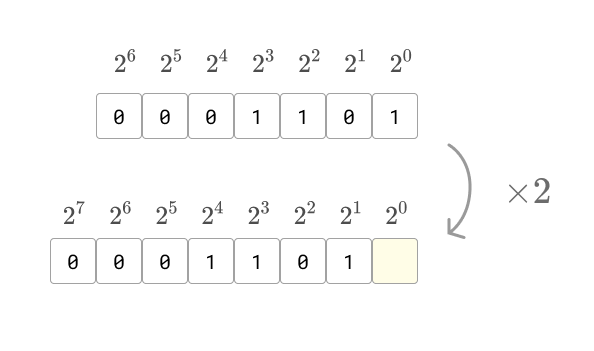 รูปประกอบการเลื่อนสตริงออกไปหนึ่งช่อง
รูปประกอบการเลื่อนสตริงออกไปหนึ่งช่อง
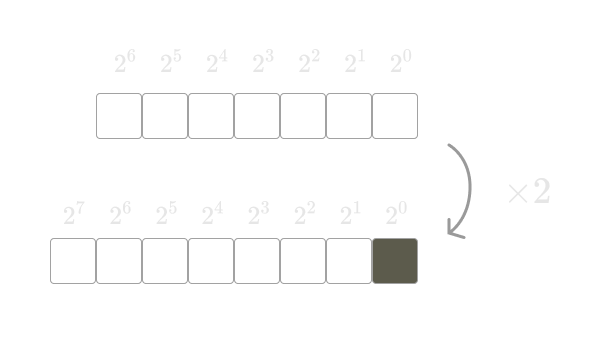 รูปประกอบการเลื่อนสตริงออกไปหนึ่งช่อง
รูปประกอบการเลื่อนสตริงออกไปหนึ่งช่อง
- บวกด้วยค่าเลขที่ถูกหมุนมาท้ายสุด เพื่อเปรียบเสมือนต่อท้ายสตริงด้วยเลขนั้น (เพิ่มขนาดสตริงจาก เป็น )
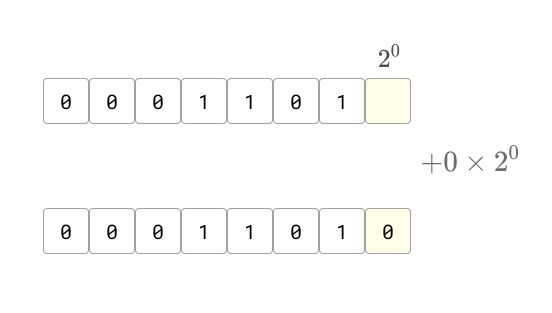 การเติมค่าเข้าไปให้ช่องสุดท้าย
การเติมค่าเข้าไปให้ช่องสุดท้าย
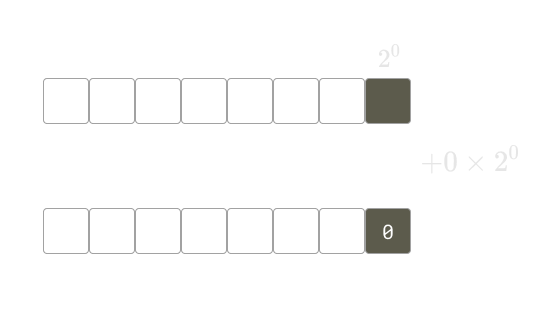 การเติมค่าเข้าไปให้ช่องสุดท้าย
การเติมค่าเข้าไปให้ช่องสุดท้าย
- ลบด้วยค่า คูณเลขหลักซ้ายสุด เพราะเราจะลดขนาดสตริงจาก เป็น เหมือนเดิม
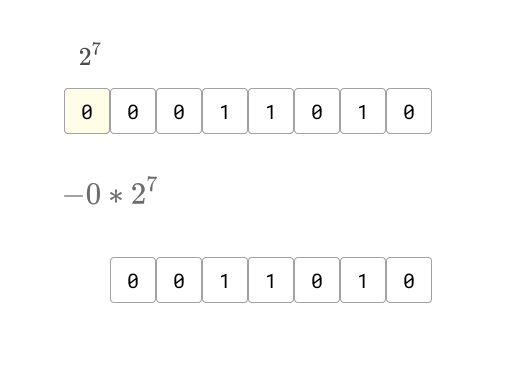 ผลลัพธ์สุดท้ายหลังจากหมุนเสร็จ
ผลลัพธ์สุดท้ายหลังจากหมุนเสร็จ
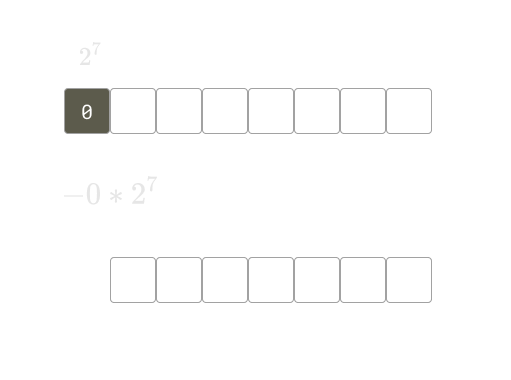 ผลลัพธ์สุดท้ายหลังจากหมุนเสร็จ
ผลลัพธ์สุดท้ายหลังจากหมุนเสร็จ
กลายเป็นว่าเราคำนวณค่า ที่เป็น แค่ตอนแรก ส่วนรอบที่เหลืออีก รอบจะทำตามขั้นตอน 3 อันด้านบน ซึ่งถ้าเก็บค่า ไว้แล้ว จะคิดค่านี้ได้ใน ต่อการหมุนสตริง 1 ครั้งแทน
ซึ่งจะเห็นว่าการที่ให้ตัวอักษรทางซ้ายมีค่ามากสุดเนี่ยทำให้การเลื่อนไปหนึ่งช่องทำได้ง่าย (ก็คือแค่คูณ 2 เข้าไปเลย) และการลบตัวหน้าสุดก็แค่ลบ ค่า คูณตัวหน้าสุดได้เลย
หลังจากนั้นเราก็เอาค่า Hashing เหล่านี้ไปเทียบสตริงเริ่มต้น ถ้าอันไหนค่าตรง เราก็ตอบจำนวนการหมุนตอนนั้นได้เลย ซึ่งในส่วนนี้หลักการจะเหมือนกับ Rabin-Karp Algorithm
ปัญหาการ Collision
ถ้าได้อ่านบทความ Rabin-Karp Algorithm ไปแล้ว เราจะเจออยู่ปัญหานึง คือเมื่อจำนวนสตริงที่เป็นไปได้มีปริมาณเยอะ เลข Hash ที่เราสามารถเอาแทนได้เนี่ยมันมีไม่พอ
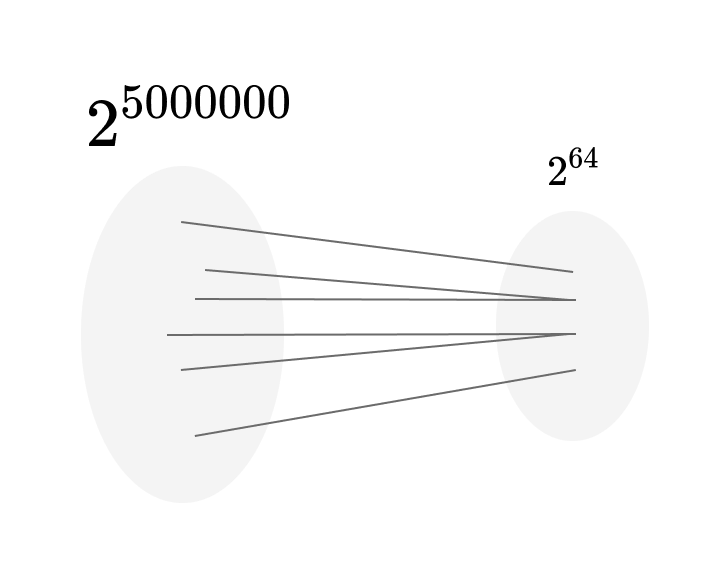 รูปเซตแทนปริมาณจำนวนสตริง เทียบกับค่า Hash
รูปเซตแทนปริมาณจำนวนสตริง เทียบกับค่า Hash
 รูปเซตแทนปริมาณจำนวนสตริง เทียบกับค่า Hash
รูปเซตแทนปริมาณจำนวนสตริง เทียบกับค่า Hash
มันจะเกิดปัญหาการ Collide ของการ Hash เกิดขึ้น ซึ่งก็คือเมื่อสตริงสองตัวมัน Hash ออกมาแล้วได้เลขเดียวกัน ซึ่งมันแปลว่าถึงได้ค่า Hash มาตรงกัน ก็ไม่ได้แปลว่าสตริงที่ดูอยู่จะเป็นค่าเดียวกัน
และด้วยความที่ค่า ในโจทย์ข้อนี้สูงมากๆ ทำให้เราต้องหาวิธีอื่นๆมาเสริมเพื่อให้การ Hash ของเรามันเสถียรยิ่งขึ้น (หรือก็คือให้โอกาสที่ Hash ออกมาแล้วได้เลขเหมือนกันมันน้อยลง)
โดยหลักๆแล้วจะมีอยู่สองวิธีที่ใช้กันบ่อยๆคือ:
- Modulo ค่า Hash ด้วยค่าจำนวนเฉพาะที่มีค่ามากๆหน่อย
เนื่องจากว่าการทำ Modulo ด้วยจำนวนเฉพาะเนี่ยจะช่วยให้ค่า Hash ออกมามีความกระจายมากขึ้นและโอกาสที่จะ Modulo ออกมาได้ค่าเหมือนกันในทุกๆ การ Mod จะน้อยลงไปเยอะ
- ใช้เลขหลายๆฐานมาทำ Hash ด้วย
ในแบบนี้คือ แทนที่จะทำด้วยฐาน 2 อย่างเดียว เราก็อาจจะเพิ่มฐานอื่นๆเข้าไปด้วย เช่น ลองฐาน 3, 7 ก็ได้ ซึ่งก็แนะนำให้ใช้จำนวนเฉพาะเป็นฐานอยู่ดี เพราะค่า Hash ที่ได้จะกระจายกันมากกว่าใช้เลขอื่นๆ
ในข้อนี้เลือกทำอย่างในอย่างนึงก็พอ แต่ถ้าจำเป็นใช้สองวิธีผสมๆกันก็ได้ เพื่อให้ลดโอกาสการ Collision ไปได้เยอะๆ
Conclusion
ข้อนี้ใช้หลักการ Rolling Hash ของ Rabin-Karp Algorithm ได้ แต่ต้องเพิ่มการ Modulo หรือ การแปลงด้วยเลขฐานอื่นเข้าไปเพื่อที่จะลดโอกาสการ Collide ของค่า Hash เยอะๆ เพราะจำนวน สตริงที่เป็นไปในข้อนี้มีเยอะมาก
ส่วนที่เหลือก็เปรียบเทียบตัวเลขตามปกติได้เลย
จริงๆ แล้วข้อนี้มีวิธีแก้ได้อีก 2 วิธี แต่จะค่อนข้างเฉพาะทางคือ
-
สังเกต pattern ว่าสตริงย่อยมีการซ้ำกันทุกๆ กี่ตำแหน่ง แล้วใช้ตัวประกอบของ มาหาสตริงย่อยขนาดเท่านั้นเพื่อลดเวลาการตรวจสอบทุกสตริง
-
ใช้ KMP Algorithm ในการทำ String matching แทน Rabin-Karp เพื่อตัดปัญหาเรื่อง Hashing ออกไปเลย
ซึ่งทั้งสองวิธีก็มี performance ใกล้เคียงกัน และทำผ่านได้ทั้งคู่
Extra Challenge
-
ถ้า operation การหมุนต้องทำ ครั้งพร้อมกันถึงจะได้อีกสตริง จะคิดแตกต่างจากเดิมยังไงบ้าง
-
ถ้าถามว่าจากการหมุนทั้งหมด ครั้งจะมีสตริงที่แตกต่างทั้งหมดกี่อัน จะคิดแตกต่างจากเดิมยังไงบ้าง