วิเคราะห์โจทย์ TOI17 ข้อ Junction
โจทย์
มีเมืองทั้งหมด เมือง หมายเลข 0 ถึง มีถนนทั้งหมด เส้น ถนนแต่ละเส้นมีค่า และจะเชี่อมโยงกันในลักษณะ tree โดยที่ เมืองแต่ละเมืองจะมีถนนเชื่อมไปหาอีกเมืองได้ไม่เกิน 3 เส้น
โจทย์ต้องการให้เราแบ่งถนนใน tree ต้นนี้ออกเป็น 3 กลุ่ม โดยที่แต่ละกลุ่มต้องเชื่อมถึงกันได้ และให้ผลรวมของค่าถนนในกลุ่มที่น้อยที่สุดนั้น มีค่ามากที่สุดเท่าที่ทำได้
โจทย์อยากรู้ว่าถ้าแบ่งกลุ่มถนนให้ดีที่สุดแล้ว ผลรวมของค่าถนนในกลุ่มที่น้อยที่สุดนั้นคือเท่าไหร่
ข้อมูลนำเข้า
บรรทัดแรก ระบุจำนวนเต็ม แทนจำนวนถนนทั้งหมด ()
บรรทัดต่อมา ระบุจำนวนเต็ม 3 จำนวน
แทนมีถนนระหว่างเมืองที่ และ และมีค่า ()
ข้อมูลส่งออก
มีบรรทัดเดียว ผลรวมของค่าถนนในกลุ่มที่น้อยที่สุด หากแบ่งกลุ่มถนนให้ดีที่สุดแล้ว
ตัวอย่างข้อมูลนำเข้าและข้อมูลส่งออก
| Input | Output |
|---|---|
| 8 0 1 9 1 2 8 2 3 11 3 4 50 4 5 1 3 6 13 6 7 12 6 8 32 | 41 |
| 5 2 3 10 2 4 13 5 3 8 0 1 30 1 2 45 | 30 |
| 7 1 2 100 2 3 99 3 4 102 2 5 1 3 0 2 5 6 1 6 7 10 | 101 |
วิเคราะห์โจทย์
ข้อนี้มีเรื่องให้น่าสังเกตอย่างนึงคือ กราฟ ที่โจทย์ให้มามันไม่ได้เป็นกราฟปกติ แต่มันมีเส้นเชื่อมเท่ากับจำนวนโหนด - 1 พอดี และด้วยความที่กราฟมันเชื่อมถึงกัน จากข้อมูลสองตัวนี้เราสามารถสรุปได้ว่า กราฟนี้มีลักษณะเป็นต้นไม้แน่ๆ
ลักษณะของกราฟในโจทย์
นอกจากส่วนที่มันเป็นต้นไม้แล้ว อีกจุดนึงที่โจทย์ให้มาคือแต่ละโหนดเชื่อมกับโหนดอื่นมากสุดแค่ 3 โหนด แปลว่า degree มากสุดของกราฟนี้คือ 3
ถ้าเรามองโหนดแต่ละ degree เราจะได้ว่าหน้าตาของแต่ละแบบจะเป็นแบบนี้:
- degree 1: โหนดจะเชื่อมกับแค่อีกโหนดเดียวเท่านั้น
 โหนด degree 1
โหนด degree 1
- degree 2: โหนดนี้จะไปเชื่อมกับอีกสองโหนด
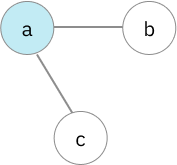 โหนด degree 2
โหนด degree 2
- degree 3: ก็เหมือนกันแหละ แค่เชื่อมได้กับอีก 3 ตัว
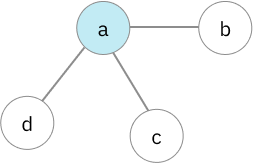 โหนด degree 3
โหนด degree 3
แล้วมันแปลว่าอะไรล่ะ?
สมมติว่าเราลองลากเส้นๆนึงจากสองโหนดที่มี degree 1 เข้าหากัน แล้วลองทำให้มันกลายเป็นเส้นตรง ถ้าไปดูตัวอย่างแรกของข้อนี้เราจะได้กราฟเดิมที่หน้าตาใหม่เป็นแบบนี้
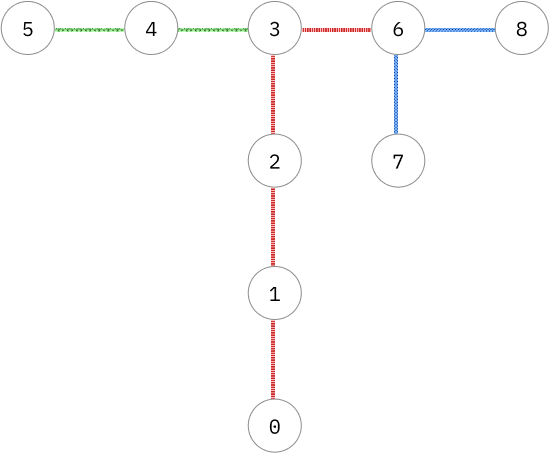 ถ้าลองลากเส้นจากโหนด 5 ไปโหนดหมายเลข 8 เป็นเส้นตรง แล้วปล่อยที่เหลือลงด้านล่าง
ถ้าลองลากเส้นจากโหนด 5 ไปโหนดหมายเลข 8 เป็นเส้นตรง แล้วปล่อยที่เหลือลงด้านล่าง
โดยสีในรูปแบ่งตามกลุ่ม ให้เป็น 3 กลุ่มที่ดีที่สุดแล้วนะ
แล้วจะแบ่งต้นไม้นี้เป็นสามส่วนยังไง?
ก่อนจะไปดูวิธีแบ่งที่มันใช้ได้ เดี๋ยวมาลองค่อยๆขยายตัวอย่างเพื่อค่อยๆดูวิธีคิดละกัน
ถ้าเราลองสมมติว่ากราฟตัวอย่างนี้เป็นเส้นตรงอย่างเดียว วิธีการแบ่งที่เป็นไปได้ก็จะเป็นว่าจุดตัดก็จะต้องอยู่บนเส้นนั้นแหละ โดยโหนดที่เป็นตัวแบ่งทั้ง 2 โหนดยังไงก็อยู่บนเส้นนี้
 ตัวอย่างกราฟที่เป็นเส้นตรง
ตัวอย่างกราฟที่เป็นเส้นตรง
แล้วถ้าเส้นตรงที่ว่านี้มีกิ่งอะไรออกมานิดหน่อยแค่โหนดเดียวแบบนี้ล่ะ จะตัดยังไงดี?
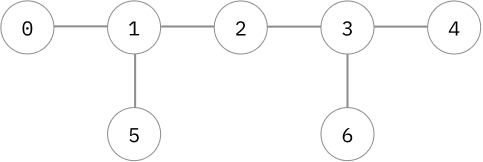 ไม่เป็นเส้นตรงละ มีโหนดห้อยมาหน่อยนึง
ไม่เป็นเส้นตรงละ มีโหนดห้อยมาหน่อยนึง
ถ้าเราลองสังเกตแค่โหนดบนเส้นตรงข้างบนกราฟ โดยไม่สนใจโหนดที่กิ่งเลย(เดี๋ยวจะรู้เองว่าทำไมไม่ต้องสนใจที่กิ่ง) มันจะมีความเป็นไปได้ในการแบ่งสีอยู่ 2 แบบ
- ไม่มีการแบ่งสีที่โหนดนั้น แปลว่าเส้นเชื่อมทั้งสามเส้นของโหนดๆนั้นจะอยู่ในกลุ่มเดียวกัน
- มีการแบ่งกลุ่มที่โหนดนั้น ซึ่งในกรณีนี้จะมีการแบ่งออกเป็นเคสย่อยได้อีก 4 แบบ
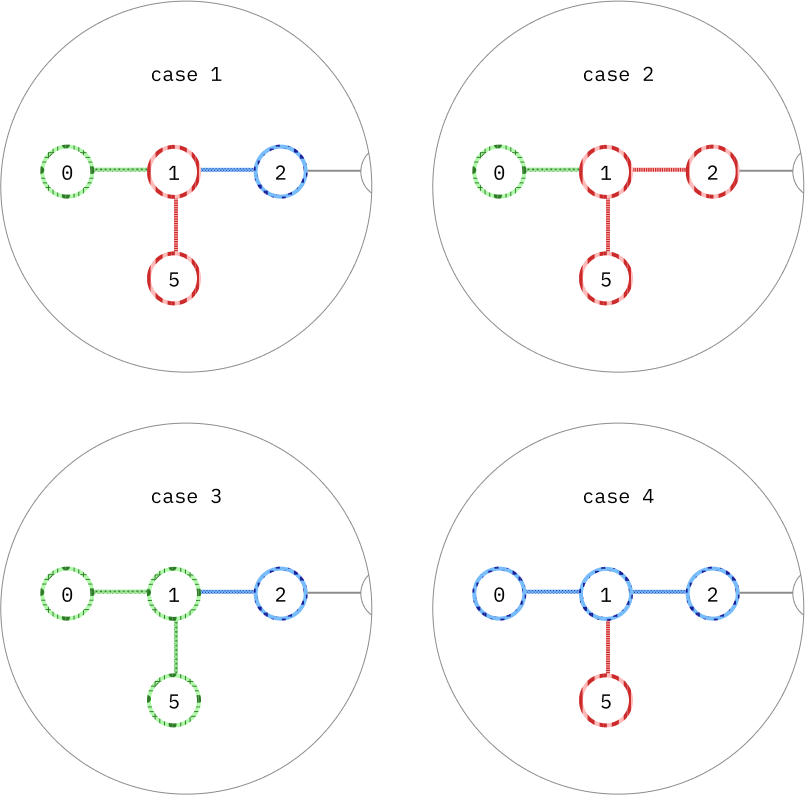 การแบ่งกลุ่มที่สามารถเกิดขึ้นได้ที่โหนดบนเส้นตรง
การแบ่งกลุ่มที่สามารถเกิดขึ้นได้ที่โหนดบนเส้นตรง
จากที่เราพอรู้ละว่ามันแบ่งแบบนี้ได้ แปลว่าถ้าเราลองค่อยๆไล่จากโหนดซ้ายไปขวาตามเส้นหลักแล้วค่อยๆเช็กกิ่งไปเรื่อยๆว่าควรอยู่ในกลุ่มเดียวกันไหม โดยที่เริ่มจากการเช็กเส้นทางซ้าย แล้วไปดูกิ่งแล้วก็ค่อยไปดูเส้นทางขวาต่อ หลังจากนั้นก็ทำแบบนี้ไปเรื่อยๆกับทุกโหนดบนเส้นหลัก
Binary Search บนคำตอบ
เราพอจะรู้แหละว่าเราต้องตัดสักที่นึงบนเส้นโหนดนั้นแหละ แต่คำถามที่ตามมาเลยคือจะไปตัดตอนไหนที่โหนดไหนล่ะ
แต่ก่อนจะไปดูว่าตัดที่ไหน ลองแวบมาดูสิ่งที่ใกล้เคียงกันนิดหน่อยก่อนดีกว่าว่า “ตัดที่ค่าเท่าไหร่ดี”
คือที่เราย้อนกลับมาดูค่านี้เนี่ยมีเหตุผล 2 อย่าง:
- มันเป็นค่าที่ส่งผลกับคำตอบที่เราต้องการ
- มันมีลักษณะพิเศษอีกอย่างนึง คือมันสามารถเอาไปใช้ทำ Binary Search ต่อได้
สมมติว่าคำตอบของโจทย์นี้คือ แปลว่า ตามโจทย์แล้วเราสามารถแบ่งกราฟออกเป็น 3 ส่วน ที่แต่ละส่วนที่แบ่งมามีผลรวม ไม่น้อยกว่า และมีส่วนนึงเท่ากับ เลย
แปลว่าในลักษณะเดียวกัน ถ้าเราลองถามว่าสามารถแบ่งกลุ่มให้ทุกกลุ่มมีค่ามากกว่า โดยที่ ได้ไหม มันก็สมควรจะต้องทำได้ใช่ไหมล่ะ ก็ขนาดแบ่งด้วย ยังทำได้เลยหนิ
แปลว่าถ้าเราลองเอามาพล๊อดเป็นเส้นดูว่าค่าไหนสามารถแบ่งได้บ้าง มันก็จะมีลักษณะเป็นแบบนี้

พอเรารู้ว่ามันแบ่งแบบนี้ได้ แทนที่เราจะพยายามหาค่า ที่ดีที่สุดไปเลย เราสามารถทำ Binary Search แล้วถามแค่ว่าแบ่งได้ไหมแทน
เพราะถ้าเราลองใช้ค่า แล้วมันแบ่งได้ แปลว่าค่าคำตอบ ที่เราต้องการมันไม่น้อยกว่า แน่ๆ
ส่วนถ้าลองแล้วแบ่งไม่ได้ ก็แปลว่าคำตอบเป็นค่าน้อยกว่า แน่ๆ
แต่ถึงรู้แล้วว่าทำ Binary Search ได้แต่จะตัดยังไงล่ะ?
วิธีที่เกือบถูก: Depth First Search (DFS) ตรงๆเลย
ไอเดียนึงที่ทำได้ จากที่เราสมมติว่ากราฟสามารถเอามาขึงเป็นเส้นตรง เราก็แค่แปะเลขกำกับไว้ไงว่าเราต้องการตรวจสอบเส้นไหนก่อน
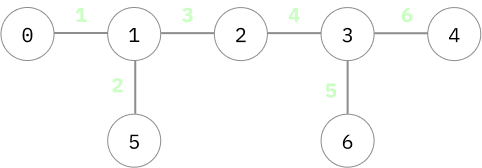 กราฟตัวอย่างที่มีกิ่งขนาดเล็กๆ
กราฟตัวอย่างที่มีกิ่งขนาดเล็กๆ
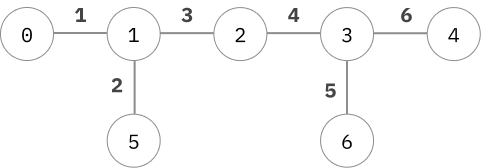 กราฟตัวอย่างที่มีกิ่งขนาดเล็กๆ
กราฟตัวอย่างที่มีกิ่งขนาดเล็กๆ
ซึ่งการจะใส่เลขมากำกับเส้นพวกนี้ก็ทำได้โดยการลองลง(traverse) ไปในกราฟแล้วค่อยๆแปะเลขด้วย Depth First Search ก็ได้
หลังจากนั้นก็เอาเส้นจากกราฟ ที่เราเรียงๆไว้มาหาเส้นตัดได้ โดยสมมติว่า ถ้าถามว่าแบ่งด้วยค่า ได้ไหม แล้วก็ไปเริ่มที่โหนดทางซ้ายสุดแล้วก็ค่อยๆลองกินเส้นตามเลขที่กำกับไว้ ถ้ารวมแล้วมันเกินค่า ไปแล้ว ก็ตัดมันทิ้ง แล้วไปเริ่มการแบ่งใหม่
ถ้าสุดท้ายตัดแล้วได้ไม่ถึง 3 ส่วน ก็แปลว่า การแบ่งด้วยค่า ที่เอามาลองมันใช้ไม่ได้ ถ้าได้ 3 ส่วนหรือมากกว่านั้นก็แปลว่าใช้ได้
ก็เหมือนจะจบแล้วมะ?
ตัวอย่างที่มันจะใช้ไม่ได้:
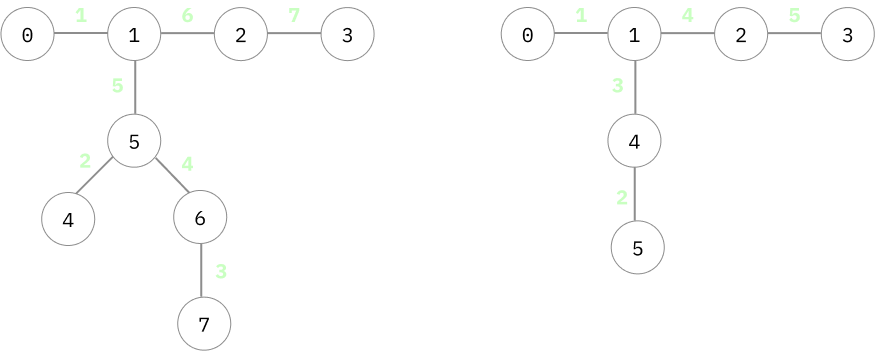 กราฟคล้ายๆเดิมที่กิ่งลึกลงไปหน่อย
กราฟคล้ายๆเดิมที่กิ่งลึกลงไปหน่อย
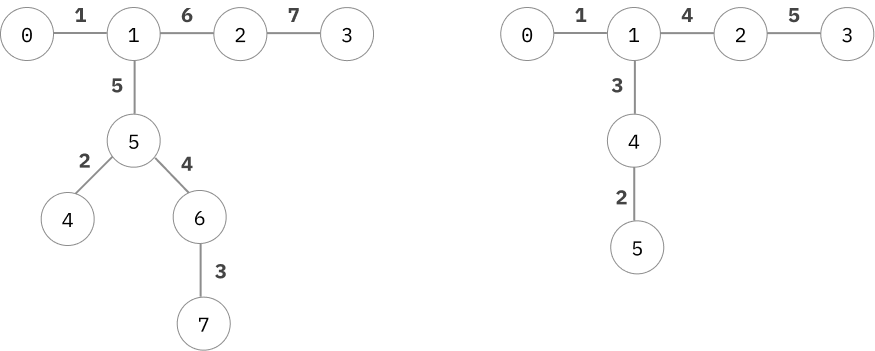 กราฟคล้ายๆเดิมที่กิ่งลึกลงไปหน่อย
กราฟคล้ายๆเดิมที่กิ่งลึกลงไปหน่อย
จะเห็นว่าการเรียงลำดับด้วย DFS ถ้ากราฟมันมีกิ่งที่ลงไปลึกๆหน่อยตามตัวอย่าง ถ้าสมมติเราไปตัด ให้เป็นส่วนนึงตอนที่เราเพิ่งดูไปแค่เส้นหมายเลข 1 กับ 2 เอง ส่วนที่ตัดออกมามันก็จะไม่ต่อกัน
อย่างในตัวอย่างทางซ้าย เราต้องเก็บไปเรื่อยๆจนถึง เส้นหมายเลข 5 แหนะกว่ามันจะเชื่อมกันหมด ซึ่งมันก็ไม่ควรจะต้องเป็นอย่างนั้น
แล้วถ้าเราดันไปตัดที่เส้นหมายเลย 2 เพราะมันใหญ่พอแล้วล่ะ? มันก็ผิดไปจากโจทย์ไง 🤣
แล้วถ้าเรายุบกิ่งที่ใหญ่ให้กลายเป็นแค่กิ่งเล็กๆได้ล่ะ?
ปัญหาของวิธีก่อนหน้า(DFS) มันอยู่ตรงที่พอกิ่งมันลงลึกๆแล้ว การเรียงเส้นกราฟมันจะเพี้ยนไป(เยอะเลยแหละ)
โอเค… งั้นถ้าเราสามารถรวบเส้นทั้งหมดภายในกิ่งตรงนั้นลงมาเหลือแค่เส้นเดียว(กิ่งขนาดโหนดเดียว) เหมือนเดิมชีวิตก็น่าจะง่ายขึ้นสินะ
ก็ใช่ แต่มันไม่ได้ง่ายขนาดนั้นเพราะคำถามใหม่ที่ตามมาอีกคือ แล้วเราจะเอาเส้นไหนเป็นเส้นหลักล่ะ?
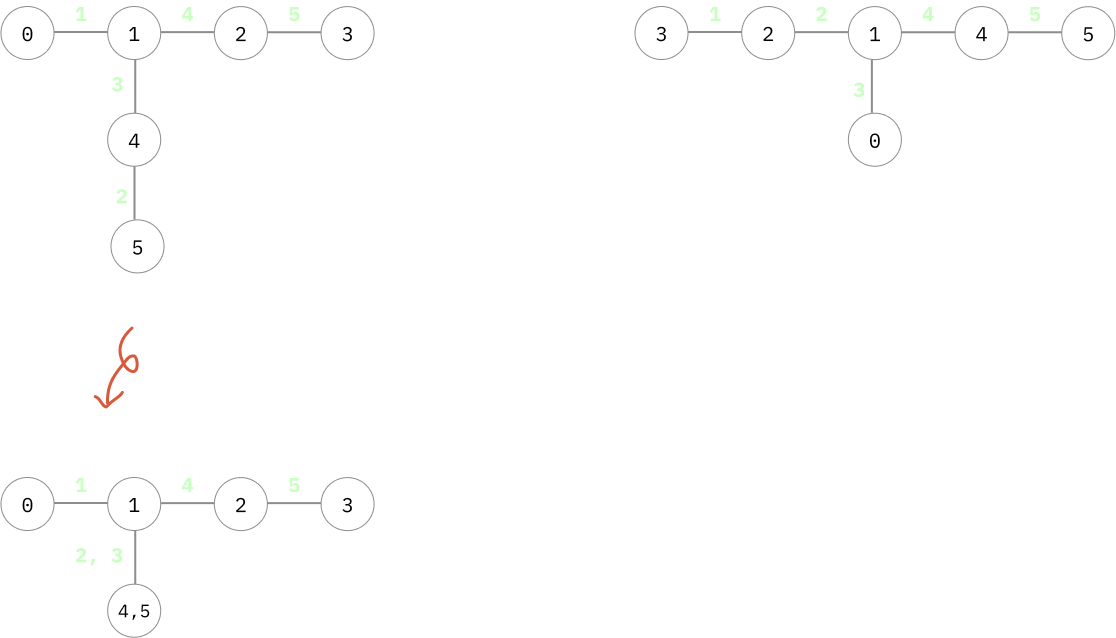 ตัวอย่างกราฟเดิมที่สามารถแปลงได้หลายแบบ ขึ้นอยู่กับว่าเลือกเส้นไหนเป็นเส้นหลัก
ตัวอย่างกราฟเดิมที่สามารถแปลงได้หลายแบบ ขึ้นอยู่กับว่าเลือกเส้นไหนเป็นเส้นหลัก
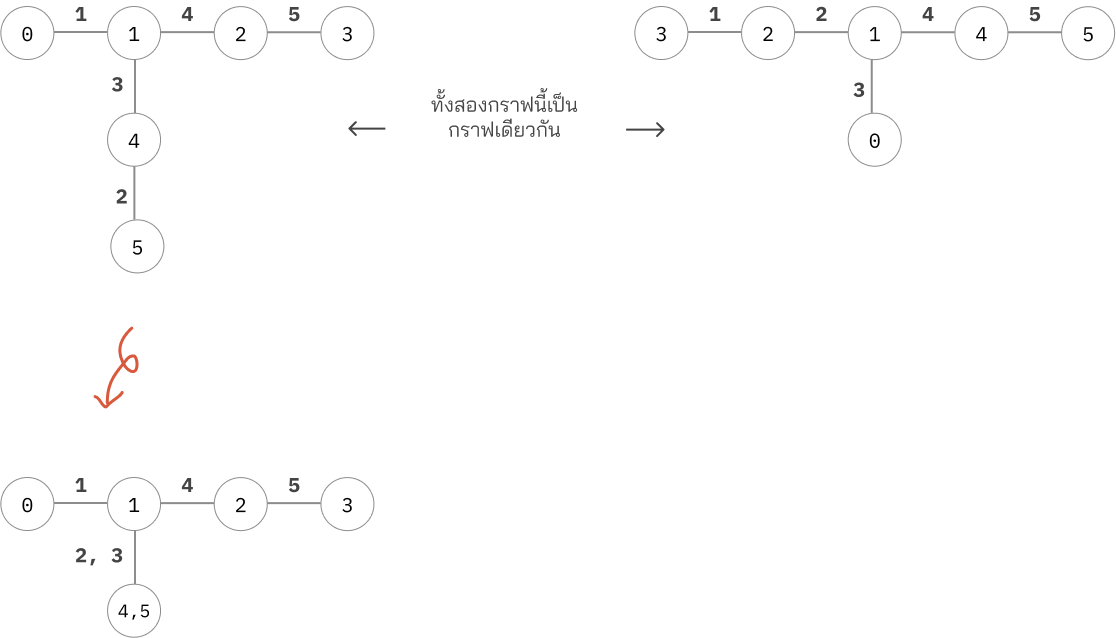 ตัวอย่างกราฟเดิมที่สามารถแปลงได้หลายแบบ ขึ้นอยู่กับว่าเลือกเส้นไหนเป็นเส้นหลัก
ตัวอย่างกราฟเดิมที่สามารถแปลงได้หลายแบบ ขึ้นอยู่กับว่าเลือกเส้นไหนเป็นเส้นหลัก
จากตัวอย่างนี้เราจะเห็นว่าถ้าเลือกเส้นตรงหลักแบบนึง ก็จะได้กิ่งมาแบบนึง ถ้าอีกแบบก็จะได้กิ่งความยาว 2 มาอีกซึ่งก็ต้องยุบให้มันเล็กลง
ดังนั้นถ้าเราเลือกเส้นหลักไม่ดี จุดที่เราต้องแบ่งกราฟมันก็อาจจะไปอยู่ที่กิ่ง แทนที่จะอยู่บนเส้นหลัก แล้วถ้าเรายุบกิ่งพวกนั้นไป เราก็จะไม่สามารถไปเช็กได้อีกเลยว่าต้องไปตัดภายในกิ่งรึป่าว
โจทย์นี้ยังดีอยู่อย่างนึงคือ ด้วยความว่าจุดตัด(จุดที่มีการแบ่งเส้น) มีได้มากสุดแค่ 2 จุด เพราะเขาต้องการแบ่งแค่ 3 ส่วน แล้วกราฟนี้ก็มี degree มากสุดแค่ 3 อีก สิ่งที่เราสรุปได้ตามมาคือ จุดตัดที่ดีที่สุดทั้ง 2 จุด จะสามารถอยู่บนเส้นเดียวกันได้ เราแค่ต้องหาให้เจอเท่านั้นเอง 😅
สุดท้ายละ(จริงๆ) แล้วจะหาเส้นหลักที่ดีที่สุดยังไง
สมมติก่อน(รอบที่เท่าไหร่แล้วก็ไม่รู้) ว่าเรารู้จุดปลายจุดนึงของเส้นที่ดีที่สุด เราก็แค่ต้องหาอีกจุดให้เจอเพื่อเชื่อมเป็นเส้นหลัก
พอเรามองตรงส่วนที่เป็นทางแยก 3 ทาง (โหนดที่มี degree 3)
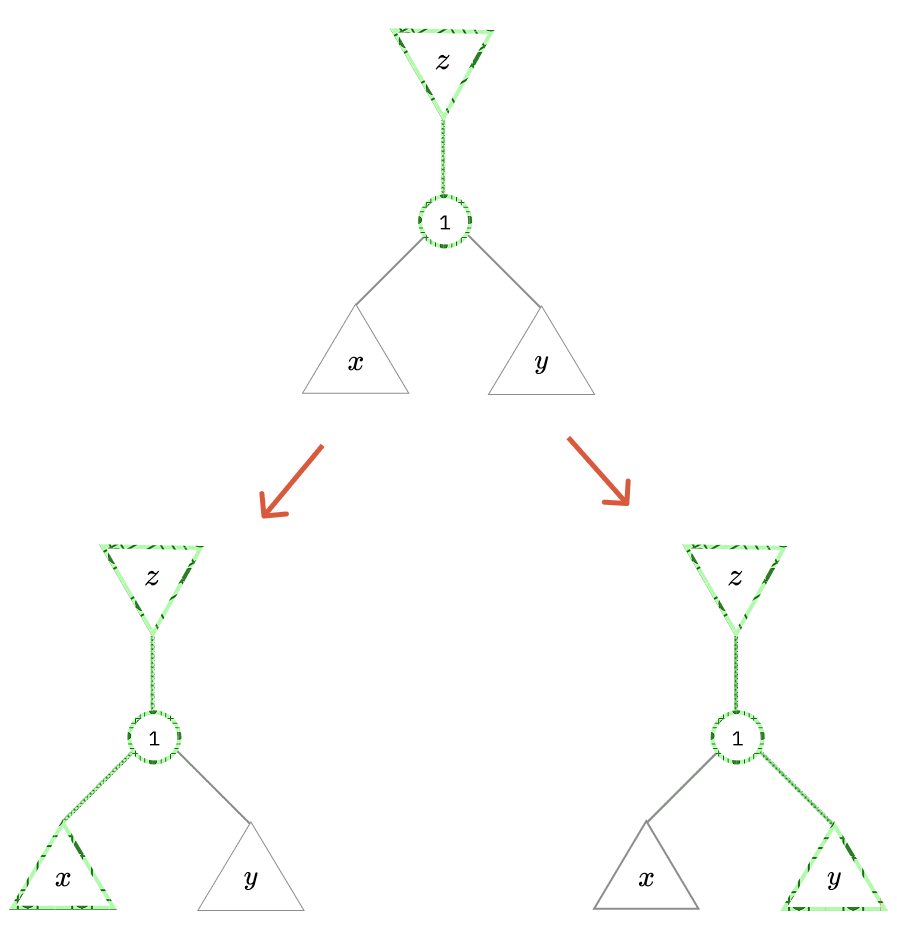 ให้ส่วน z เป็นส่วนนึงของเส้นหลัก แล้วกำลังจะหาว่าต้องไปทางส่วน x หรือ y
ให้ส่วน z เป็นส่วนนึงของเส้นหลัก แล้วกำลังจะหาว่าต้องไปทางส่วน x หรือ y
จากที่สมมติว่าเรารู้ว่าจุดด้านนึงของเส้นหลักอยู่ที่ไหน แปลว่าเราจะมีแค่ 2 ตัวเลือกให้เราคิดว่าต้องไปหาทางไหนดี ระหว่าง x หรือ y ซึ่งวิธีคิดมันก็ง่ายๆตาม common sense เลยคือไปทางที่หนักกว่าไง
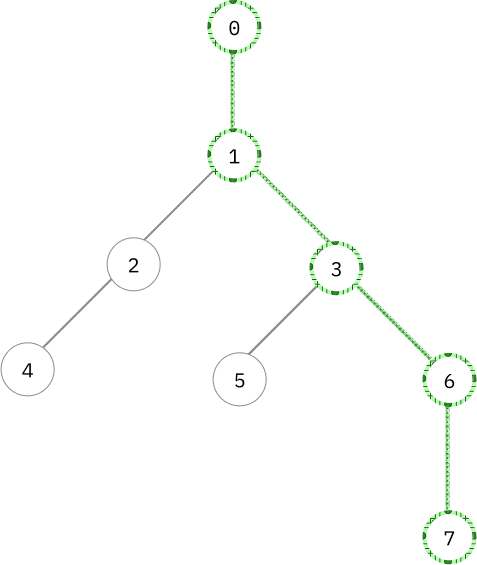 ตัวอย่างกราฟแสดงว่าควรไปทางที่หนักกว่า
ตัวอย่างกราฟแสดงว่าควรไปทางที่หนักกว่า
ทำไมถึงไปทางหนักกว่า?.. ถ้าเรารู้ว่าด้านไหนด้านนึงมันหนักกว่าอีกด้าน มันก็แปลว่าจุดตัดต้องไปอยู่ในฝั่งที่หนักกว่า เพราะว่าถ้าอยู่ฝั่งที่เบากว่าก็จะได้การแบ่งที่ไม่สมดุลมากกว่าเดิม ก็คือฝั่งที่เบาอยู่แล้วมันก็จะเบามากกว่าเดิม เพราะไปตัดถนนใกล้ส่วนที่มันเบา ก็เลยควรไปทางที่หนักกว่าแทน ดังนั้นพอเราเจอทางแยก เราก็แค่หาว่า sub-tree ไหนมันหนักกว่าก็สรุปได้แล้วว่าจุดตัดต้องไปอยู่ทางนั้น
แต่ตอนแรกเราสมมติว่าเรารู้จุดด้านนึงของเส้นนี้ใช่มะ… จริงๆแล้วเราไม่รู้หรอก เราก็เลยต้องสุ่มมั่วโหนดใบ(degree 1) สักโหนดมาก่อน แล้วลองมองหาเส้นหลักไป
ซึ่งแน่นอนว่ามันก็มีโอกาสที่โหนดที่เลือกมาตอนแรกจะไม่ถูกอีก เราก็เลยต้องมาดูอีกกรณีนึงคือ
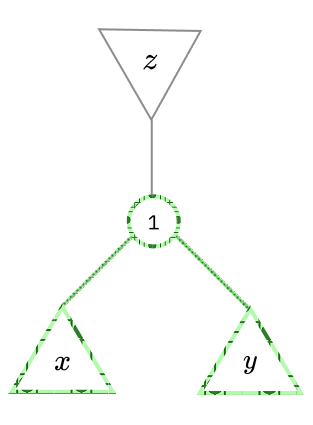 ถ้า sub-tree ตรงทางแยกมันหนักกว่าเส้นหลักที่เราเลือกมา
ถ้า sub-tree ตรงทางแยกมันหนักกว่าเส้นหลักที่เราเลือกมา
ถ้าตอนที่เรากำลังดูทางแยกอ่ะ ถ้าทั้งสอง sub-tree มันหนักกว่าต้นทางที่เราเลือกมา จากเหตุผลเหมือนตอนแรกแหละว่าจุดตัดควรจะอยู่ตรง sub-tree ที่หนักกว่า แปลว่าโหนดที่เราเลือกมาตอนแรกก็ไม่ได้อยู่บนเส้นหลักแน่ๆละ แล้วเส้นหลักจริงๆจะอยู่กับ sub-tree ทางซ้ายและขวาแทน
ถ้าเราเจอกรณีนี้ ก็จะไปเลือกใช้โหนดใบจากทั้งสองกิ่งที่เราเจอว่ามันหนักเป็นเส้นหลักแทน
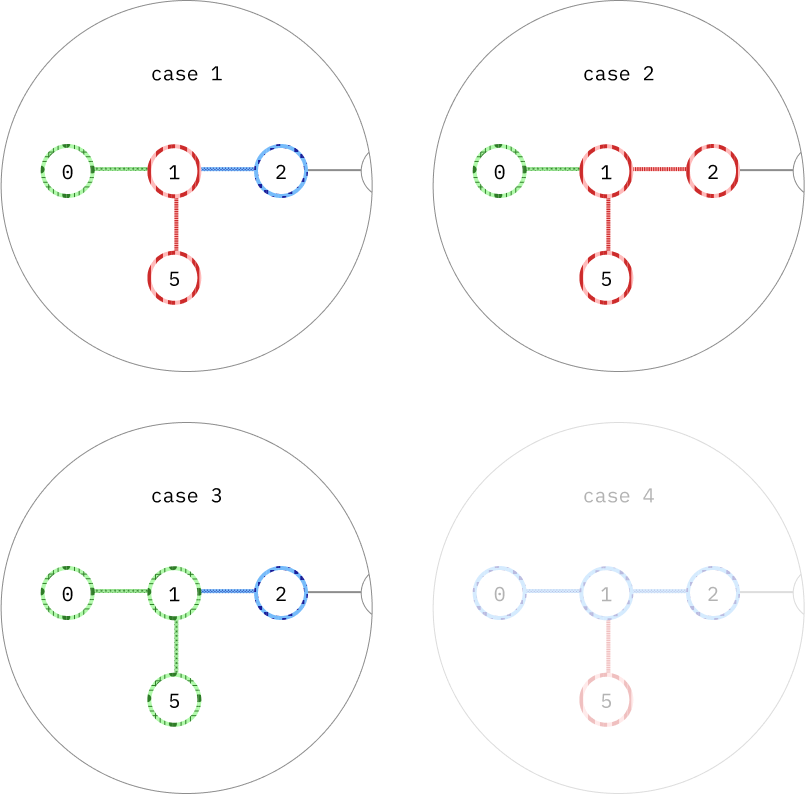 การแบ่งกลุ่มที่สามารถเกิดขึ้นได้ที่โหนดบนเส้นตรงที่ยังเป็นไปได้
การแบ่งกลุ่มที่สามารถเกิดขึ้นได้ที่โหนดบนเส้นตรงที่ยังเป็นไปได้
แค่นี้เราก็จะได้เส้นหลักมาแล้ว ซึ่งการทำแบบนี้ก็จะตัดปัญหาของการแบ่งกลุ่มแบบที่ 4 ไปด้วย เพราะกรณีที่ 4 นี้เกิดขึ้นได้ก็ต่อเมื่อกิ่งมันหนักมากพอที่เป็นส่วนนึงออกมาเลย ซึ่งมันก็ควรจะอยู่บนเส้นหลักไปแล้วเพราะเราเลือกทางที่มันหนักกว่าอยู่แล้ว ดังนั้นการแบ่งแบบนี้มันจะเรียงใหม่จนกลายเป็นการตัดแบบอื่นๆอีก 3 แบบแทน
พอได้แบบเส้นหลักมาแล้วเราก็รวบตรงกิ่งที่มันยาวๆให้กลายเป็นเส้นเดียวกันได้ แล้วก็กลับไปทำ Binary Search บนคำตอบเหมือนเดิมได้เลย