คำนวณ Hamming Distance จากโจทย์ Programming.in.th

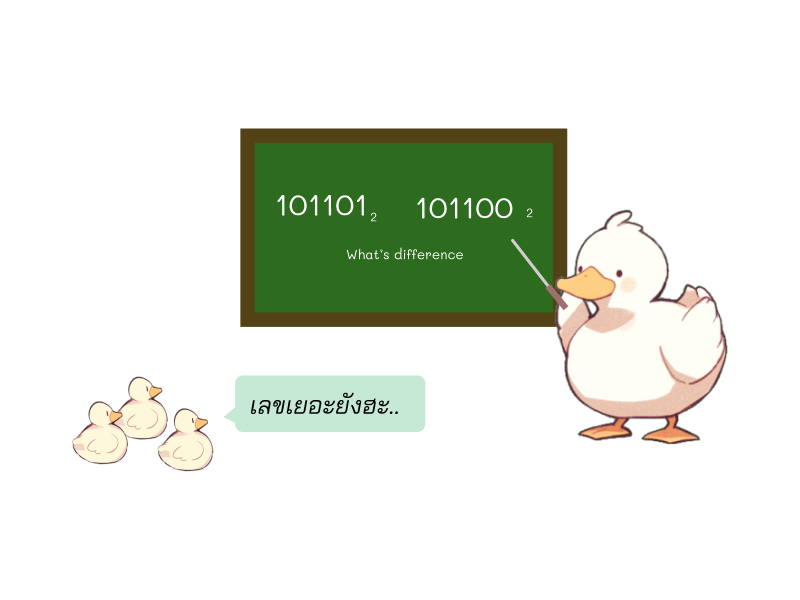
โจทย์

ความยาก ★★★☆☆
นิยาม Hamming distance คือจำนวนบิตที่แตกต่างกันในเลขฐานสองระหว่างการเทียบ 2 เลข เช่น $1010_2$ กับ $0011_2$ มี Hamming distance เป็น 2 เพราะต่างกันที่บิตแรกและบิตสุดท้าย

โจทย์จะให้ค่า $K,N$ มาให้ อยากรู้ว่าผลรวม Hamming distance สำหรับเลขฐานสองที่มี $K$ หลักของ $x-1$ กับ $x$ เมื่อ $x$ มีค่าตั้งแต่ $1$ ถึง $N$ คือเท่าไหร่

ข้อมูลนำเข้า บรรทัดแรก ระบุจำนวนเต็ม $K,N$ ($K\leq32,N\leq2^{K}-1$) แทนจำนวนหลักของเลขฐานสองและช่วงของค่าที่ดู

ข้อมูลส่งออก แสดงค่าผลรวมของ Hamming distance

ตัวอย่างข้อมูลนำเข้าและข้อมูลส่งออก

คำอธิบายตัวอย่างแรก:

$K=3$ และ $N=4$ แปลว่าเราต้องดูเลข $3$ หลัก ตั้งแต่ $0$ จนถึง $4$ ที่คำนวณได้ดังนี้

• $000_2$ และ $001_2$ มี Hamming Distance เท่ากับ $1$
• $001_2$ และ $010_2$ มี Hamming Distance เท่ากับ $2$
• $010_2$ และ $011_2$ มี Hamming Distance เท่ากับ $1$
• $011_2$ และ $100_2$ มี Hamming Distance เท่ากับ $3$

ทำให้ผลรวมของ Hamming Distance ทั้งหมด เป็น $1+2+1+3 = 7$

วิเคราะห์โจทย์

การหา Hamming Distance

หา Hamming Distance ของเลข 2 ตัวเนี่ย เราต้องการรู้แค่ว่ามีบิตที่ต่างกันกี่ตัว ดังนั้นเราสามารถทำ xor bit ใส่เลขทั้งสองตัวได้
ในผลลัพธ์ของแต่ละบิตจะเป็นว่า ถ้าบิตของทั้งสองเลขต่างกัน ในผลลัพธ์ก็จะเป็น $1$ แต่ถ้าเหมือนกันจะเป็น $0$ ดังนั้นโจทย์ก็จะเปลี่ยนเป็นว่าหาว่ามีบิต 1 กี่ตัวแทน

ทีนี้โจทย์ก็จะเหลือแค่ นับจำนวนเลข $1$ ในผลลัพธ์ ซึ่งทำได้ใน $\mathcal{O}(log(N))$ หรือ $\mathcal{O}(1)$ แล้วแต่ว่าจะ implement ยังไง

แต่ถ้าไปอ่าน Constraint ใหม่ จะเห็นว่า $N$ เป็นได้ถึง $2^{32} - 1$ ซึ่งมันเยอะไป ค่อยๆทำทีละคู่ไม่ได้เพราะจะไม่ทันเวลาเอา

ข้อสังเกต

โจทย์ไม่ได้ถามหา Hamming Distance ของเลขมั่วๆ แต่เป็นทุกคู่ตัวเลขที่ติดกันเท่านั้น ดังนั้นเราไม่จำเป็นต้องใช้วิธีคำนวณที่รองรับทุกรูปแบบตัวเลขก็ได้

ทีนี้สังเกตเพิ่มว่า การที่ค่า Hamming Distance เท่ากับ $p$ หมายความว่าจะมีทั้งหมด $p$ บิตที่แตกต่างกัน ซึ่งแต่ละบิตเนี่ยเราสามารถคิดแยกจากกันได้ แล้วการที่ Hamming Distance เพิ่มขึ้นมา 1 ได้นั้นมาจากการเทียบเลข ที่มีบิตที่มีค่าอันนึงเป็น 0 และอีกอันเป็น 1 ถ้าเรามาดู pattern แยกทีละบิตก็จะเห็นว่า

• บิตที่ 1 จะเห็นว่าบิตจะแตกต่างกันทุกครั้งเลย สังเกตตอนคำนวณ 0,1 หรือ 1,2 หรือ 2,3 หรือทุกครั้งที่ $x$ ที่หารด้วย 1 ลงตัว(ก็คือทุกครั้งแหละ 🤣) เพราะบิตนี้จะสลับ 0 กับ 1 ในการบวกทุกครั้ง

• บิตที่ 2 จะแตกต่างกันในกรณีที่มีค่า 1,2 หรือ 3,4 หรือ 5,6 หรือ $x$ ที่หารด้วย 2 ลงตัว เพราะบิตนี้จะสลับ 0 กับ 1 ในการบวกทุกๆ 2 ครั้ง

• บิตที่ 3 ก็จะต่างกันในตอนที่มีคำนวณค่า 3,4 หรือ 7,8 หรือ 11,12 ก็คือเมื่อ $x$ ที่หารด้วย 4 ลงตัว เพราะบิตนี้จะสลับ 0 กับ 1 ในการบวกทุก 4 ครั้ง

จากการลองทดดูจะสังเกตได้ว่าสำหรับบิตที่ $q$ ใดๆ บิตนี้จะแตกต่างกันตอนที่เราเทียบ $x-1$ กับ $x$ เมื่อ $x$ หารด้วย $2^{q-1}$ ลงตัว

ดังนั้นเราสรุปได้ว่าถ้าคิดแค่บิตที่ $q$ จะมีทั้งหมด $\lfloor{\frac{n}{2^q}}\rfloor$ คู่ที่แตกต่างกัน ซึ่งเราสามารถคำนวณได้ใน $\mathcal{O}(1)$ ได้เลย

ประกอบเป็นคำตอบ

โจทย์ของเราก็จะลดรูปเหลือแค่ผลรวมของจำนวนเลขที่หารลงตัวด้วย $1,2,4,8,16,\dots$ มีทั้งหมดกี่ตัว ซึ่งหาได้จากการ loop บวกตรงๆ ของ $\lfloor{\frac{n}{2^q}}\rfloor$ ได้ ทำให้ทำได้ใน $\mathcal{O}(log(N))$

1
uint64_t HammingDistance(uint32_t n, uint8_t k)
2
{
3
  uint64_t accumulatedDistance = 0;
4
  for(uint8_t i = 0; i < k; i++)
5
    accumulatedDistance += n / (1 << i);
6
  return accumulatedDistance;
7
}

Challenge

1. ถ้าเปลี่ยนเป็นถามได้ 100000 ครั้ง และแต่ละครั้งให้ค่า $x$ เป็นได้ตั้งแต่ $a$ ถึง $b$ จะแตกต่างจากวิธีเดิมยังไงบ้าง
2. ต่อจากข้อ 1 ถ้า $K\leq 2^{64}-1$ จะแตกต่างจากวิธีในข้อ 1 ยังไงได้บ้าง

ลิงก์

ลิงก์โจทย์ Programming.in.th

https://programming.in.th/tasks/1048