วิเคราะห์โจทย์ TOI17 ข้อ Noodle
โจทย์
มีช่องทางจัดจำหน่ายเส้นขนมจีนทั้งหมด ช่องทาง(ที่ติดกันเป็นเส้นตรง) มีร้านค้าขนมจีนอยู่ทั้งหมด ร้าน
โดยช่องทางจัดจำหน่ายหมายเลข จะมีปริมาณขนมจีน
ทีนี้แต่ละร้านจะเลือกช่วงของช่องทางจัดจำหน่ายที่ติดกัน เพื่อซื้อขนมจีน
- ร้านที่ 1 ได้ช่องที่ ถึง
- ร้านที่ 2 ได้ช่องที่ ถึง
- ไปเรื่อยๆ จนถึงร้านที่ ได้ช่องที่ ถึง
โดยค่า ของแต่ละร้านเนี่ยเรากำหนดเองได้ เพื่อที่จะแบ่งช่องทางให้แต่ละร้าน
หลังจากเลือกแบ่งช่องทางให้แต่ละร้านเสร็จแล้ว แต่ละร้านจะเลือกช่องทางจัดจำหน่ายที่ได้เยอะที่สุดมาทั้งหมด ช่องทางจากช่องทางในช่วงของร้านนั้นๆเอง เพื่อเลือกรับขนมจีน
ถามว่าถ้าแบ่งช่องทางให้แต่ละร้านให้ดีที่สุดแล้ว ร้านที่มีขนมจีนน้อยที่สุดจะได้ปริมาณเท่าไหร่
โดยนิยามว่าดีที่สุดคือ ต้องการให้ร้านที่ได้รับขนมจีนน้อยที่สุดเนี่ย ได้ปริมาณขนมจีนให้ได้มากที่สุดเท่าที่เป็นไปได้
ข้อมูลนำเข้า
บรรทัดที่ 1 เป็นจํานวนเต็ม 3 จํานวน
แต่ละจํานวนถูกคั่นด้วยช่องว่าง ได้แก่
แทนจํานวนช่องทางการรับเส้นขนมจีนทั้งหมด จํานวนร้านค้า และจํานวนช่องทางการรับเส้นขนมจีน ที่แต่ละร้านค้าสามารถรับขนมจีนออกมาได้
โดยที่ และ
อีก บรรทัดถัดมา แต่ละบรรทัด มีจํานวนเต็ม แทนปริมาณเส้นขนมจีนที่เข้าไปรับได้ของช่องทางที่ โดยที่
ข้อมูลส่งออก
มีบรรทัดเดียว แสดงปริมาณรวมของเส้นขนมจีนของร้านที่ได้ขนมจีนไปน้อยที่สุด ถ้าเราจัดแบ่งช่องทางให้ได้ดีที่สุดแล้ว
ตัวอย่างข้อมูลนำเข้าและข้อมูลส่งออก
| Input | Output |
|---|---|
| 12 3 3 1 6 5 7 4 8 9 3 10 2 12 13 | 21 |
| 10 3 1 1 9 5 7 4 8 9 3 10 2 | 9 |
คำอธิบายตัวอย่างแรก:
แบ่งช่องทางการรับขนมจีนตามนี้:
- ร้านที่ 1: ช่องที่ 1 ถึง 6
- ร้านที่ 2: ช่องที่ 7 ถึง 9
- ร้านที่ 3: ช่องที่ 10 ถึง 12
ทำให้ร้านที่ 1 จะเลือกจาก ช่องทางที่ 2, 4, และ 6 เลยได้รวมเป็น 21 ที่น้อยกว่าอีก 2 ร้านที่ได้ 22 และ 27 ตามลำดับ
วิเคราะห์โจทย์
ก่อนอื่นเลย เราจะมาคิดในแบบที่มีแค่ 1 ร้านก่อน
ถ้ามีแค่ร้านเดียวมันก็ง่ายอ่ะเนอะ เราก็แค่เก็บค่ามากที่สุด ลำดับแรก แล้วเอามารวมกันเป็นคำตอบได้เลย
แต่ถ้ามีมากกว่า 1 ร้าน จะแบ่งช่องทางให้แต่ละร้านยังไงล่ะ?
พอจะแบ่งช่องทางให้แต่ละร้านมันก็ต้องมาเริ่มคิดละว่า แบ่งแค่ไหนเยอะหรือน้อยไปไหม เพราะถ้าเราไปโฟกัสกับร้านที่ได้น้อยที่สุดแล้วพยายามเพิ่มช่องทางให้เยอะๆ ร้านถัดมาก็อาจจะได้น้อยลงจนกลายเป็นร้านที่ได้น้อยที่สุดไปอีก แล้วแถมในโจทย์มีร้านต้องแบ่งตั้ง 100 ร้านก็จะวุ่นวายไปกันใหญ่
โจทย์เดิมในอีกมุมมอง
สมมติเปลี่ยนเป็นถามว่า ถ้าเราแบ่งให้แต่ละร้านได้ดีที่สุดแล้ว ร้านที่ได้ขนมจีนน้อยที่สุดยังได้ไม่น้อยกว่า รึเปล่า โดยที่ เป็นค่าที่เราสมมติขึ้นมาเอง
พอคิดแบบนี้เรื่องการแบ่งช่องทางก็จะง่ายขึ้น เพราะเราจะพยายามให้แต่ละร้านได้ความยาวช่วงที่สั้นที่สุดในขณะที่ผลรวมค่ามากที่สุด ลำดับแรกยังไม่น้อยกว่า
 Label ของสัญลักษณ์ที่ใช้
Label ของสัญลักษณ์ที่ใช้
 Label ของสัญลักษณ์ที่ใช้
Label ของสัญลักษณ์ที่ใช้
 มี 2 ร้าน ค่า P = 30 แบ่งร้านแรก 3 อันแรก (ยาวเกินความจำเป็น)
มี 2 ร้าน ค่า P = 30 แบ่งร้านแรก 3 อันแรก (ยาวเกินความจำเป็น)
 มี 2 ร้าน ค่า P = 30 แบ่งร้านแรก 3 อันแรก (ยาวเกินความจำเป็น)
มี 2 ร้าน ค่า P = 30 แบ่งร้านแรก 3 อันแรก (ยาวเกินความจำเป็น)
สังเกตว่า ถ้าแบ่งช่องทางให้ร้านแรกได้ 3 ช่องเลย จะทำให้ร้านหลังๆ ได้ช่องทางที่เหลือไม่พอ เพราะร้านแรกเลือกช่องทางที่มีค่าขนมจีนสูงไปแล้ว ทำให้ร้านหลังๆ เลือกได้แค่ช่องทางที่เหลือที่มีค่าขนมจีนต่ำกว่า
ทั้งๆที่ ร้านแรกสามารถเลือกช่องน้อยกว่านั้นได้
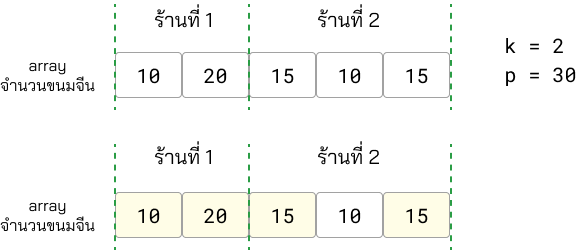 มี 2 ร้าน ค่า P = 30 แบ่งร้านแรก 2 อันแรก (แบ่งแบบยาวน้อยสุด)
มี 2 ร้าน ค่า P = 30 แบ่งร้านแรก 2 อันแรก (แบ่งแบบยาวน้อยสุด)
 มี 2 ร้าน ค่า P = 30 แบ่งร้านแรก 2 อันแรก (แบ่งแบบยาวน้อยสุด)
มี 2 ร้าน ค่า P = 30 แบ่งร้านแรก 2 อันแรก (แบ่งแบบยาวน้อยสุด)
สาเหตุที่วิธีแบ่งช่วงแบบนี้ทำได้ดีที่สุดเพราะ ถ้าร้านแรกๆ เลือกใช้ช่องทางน้อย ร้านหลังๆ ก็จะมีโอกาสเลือกช่องที่มีค่าขนมจีนสูงได้มากขึ้น
การเพิ่ม/ลดค่า P
จริงๆ แล้วการเลือกค่า มีผลต่อความยาวช่องของแต่ละร้านที่เลือก
- ถ้าค่า น้อยจะทำให้แต่ละร้านเลือกช่วงสั้นๆ และเหลือช่วงให้ร้านสุดท้ายเยอะเกินความจำเป็น
- ถ้าค่า เยอะจะทำให้แต่ละร้านต้องเลือกช่วงยาวๆ เพื่อให้ได้มากให้ครบค่า ทำให้ร้านท้ายๆ มีช่องเลือกได้ไม่พอ
 มี 4 ร้าน P = 12 (ค่า P น้อยๆ)
มี 4 ร้าน P = 12 (ค่า P น้อยๆ)
 มี 4 ร้าน P = 12 (ค่า P น้อยๆ)
มี 4 ร้าน P = 12 (ค่า P น้อยๆ)
การเลือกค่า น้อยๆ จะทำให้ร้านแรกๆ เลือกช่วงสั้นๆ ทำให้ร้านหลังๆ เลือกได้ช่องทางที่เหลือเยอะเกินความจำเป็น แต่อย่างน้อยก็ยังแบ่งช่องทางให้ร้านสุดท้ายได้ แค่ค่าของร้านแรกๆ จะได้น้อยเกินกว่าที่โจทย์ต้องการ
แต่ถ้าลองใหม่ด้วยการเลือกค่า ที่สูงขึ้นล่ะ
 เปลี่ยนไปใช้ค่า P สูงๆ
เปลี่ยนไปใช้ค่า P สูงๆ
 เปลี่ยนไปใช้ค่า P สูงๆ
เปลี่ยนไปใช้ค่า P สูงๆ
พอค่า สูงเกินไป ร้านแรกๆ ก็จะเลือกช่วงยาวขึ้น แต่ทำให้ร้านหลังๆ เลือกได้ช่องทางที่เหลือน้อยลง แถมบางร้านไม่พอเลือกช่องทางเลยด้วยซ้ำ
พอคิดได้แบบนี้เราก็แค่ต้องหาค่า ที่มากที่สุดเพื่อเอาไปตอบคำถามในโจทย์เริ่มต้น
แต่ปัญหามันติดอยู่ที่ว่า ค่าขนมจีนแต่ละช่องมันสูงไปหน่อย(ตั้ง 500,000) ทำให้ถ้าจะลองเพิ่มค่า ทดลองไปเรื่อยๆตรงๆ เช่นลองเพิ่มทีละ 1 จะใช้เวลาในการคำนวณมากเกินไป
คำนวณค่าผลรวม K ตัวในช่วงยังไง
มีหลายวิธีให้เลือกแหละ แต่วิธีง่ายสุดก็คงเป็นการใช้ Multiset มาเก็บค่าที่มากที่สุดทั้ง ตัวไว้ แล้วพอมีค่าใหม่ก็เอาไปเทียบกับค่าในนั้นว่าค่าใหม่มากกว่าอะไรไหม
ถ้ามากกว่าก็ดึงค่าที่น้อยที่สุดใน Multiset ออกมา แล้วก็ทำแบบเดิมไปเรื่อยๆ
การเลือกค่า P
เราจะ Binary search ค่า และเอาค่า ที่ว่า ไปแบ่งช่วงต่อโดยให้แต่ละร้านได้ความยาวช่วงสั้นที่สุด แล้วดูว่าเกิดอะไรขึ้นบ้าง
- ถ้ายังแบ่งได้ทุกร้าน เราจะเพิ่มค่า เพื่อให้พยายามใช้ทุกช่องทางให้คุ้ม แล้วเก็บค่า ที่ทำได้ไว้
- ถ้าแบ่งไม่ได้ ด้วยเหตุผลว่าเลือกมากที่สุด ลำดับแล้วยังค่าไม่ถึง หรือแบ่งได้ไม่ถึงร้านสุดท้าย เราจะลดค่า เพื่อให้แบ่งให้ร้านหลังๆ ได้
หลังจากทำขั้นตอนนี้เสร็จแล้ว เราก็จะเอาค่า ที่มากที่สุดมาตอบได้เลย
และด้วยความว่าเราแค่ Binary search บนค่าผลรวมของขนมจีน ทำให้ต้องเช็กค่า จริงๆแค่ ครั้งก็พอ
Time Complexity:
Memory Complexity:
Extra Challenge
- ถ้าแต่ละร้านมีค่า เป็นของตัวเอง จะคิดแตกต่างจากวิธีเดิมยังไงบ้าง
- ถ้าเปลี่ยนค่า เป็นตั้งแต่ 1 ถึง แล้วให้ตอบทุกค่า จะคิดแตกต่างจากวิธีเดิมยังไงบ้าง




