Practical Algorithms Logo Practical Algorithms
• 4 min

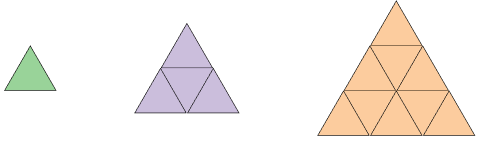
โจทย์พีระมิด Genwit

ยังจำข้อพีระมิดของ #Genwit รอบชิงกันได้อยู่ไหม วันนี้เราเอามันมาอธิบายเพิ่มให้เห็นภาพชัดขึ้นหน่อย ถ้าเข้าใจแล้วโจทย์นี้ไม่ได้ยากเลย ทุกคนก็ทำได้

เป็ดไอคอนของเรื่องเล่าชาวอัลกอ Practical Algorithms
Practical Algorithms: เรื่องเล่าชาวอัลกอ
เพจที่อยากให้คนไทยมีเนื้อหาอัลกอริทึมดีๆ ให้ได้อ่านกัน
Math Pre-Posn
เป็ดของชาวอัลกอกำลังแบกอิฐขึ้นไปสร้างพีระมิด และพูดว่าอิฐมาเพิ่มแล้ว

โจทย์

ในการสร้างพีระมิดที่ฐานสี่เหลี่ยมจัตุรัสที่ กว้างและยาว 230.1 เมตร

ถ้าจะสร้างพีระมิดโดยใช้อิฐขนาด 30×30×1930\times30\times19 ซม. เป็นด้านกว้าง, ยาว และ สูง ตามลำดับ
โดยให้ชั้นถัดๆไป (โดยเริ่มจากที่ฐาน) จะใช้อิฐทั้งสี่ด้าน น้อยลงด้านละ 1 แถว ถามว่าจะต้องใช้อิฐทั้งหมดกี่ก้อนในการสร้างพีระมิดดังกล่าว

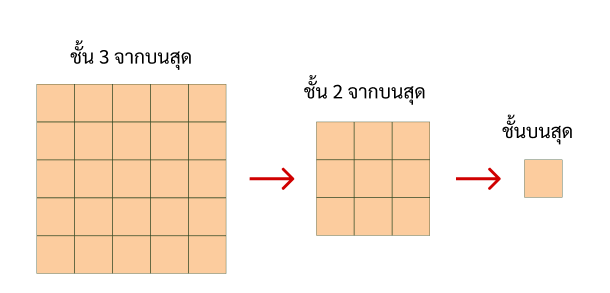ชั้นบนสุดเป็นขนาด 1 คูณ 1 ถัดไปเป็น 3 คูณ 3 ถัดลงไปอีกเป็น 5 คูณ 5 ขนาดของพีระมิดแต่ละขั้น

เฉลย

  • ขั้นที่ 1

    ก่อนอื่นเลยเราต้องรู้ก่อนว่าที่ฐานของพีระมิดเนี่ยต้องใช้อิฐด้านละเท่าไหร่

    จากโจทย์บอกว่าที่ฐานยาวด้านละ 230.1 เมตร เท่ากัน และอิฐแต่ละก้อนยาวแค่ 0.3 เมตร (30 ซม.)
    เราเลยสามารถคำนวณได้ว่าจะต้องใช้อิฐด้านละ 230.10.3=767\frac{230.1}{0.3}=767 ก้อน

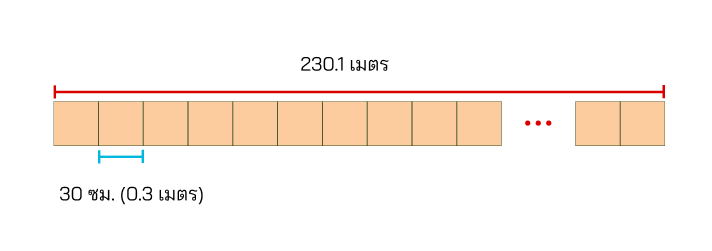ชั้นล่างสุดที่ยาว 230.1 เมตรที่เกิดจากการวางอิฐชิ้นเล็กต่อๆกัน วิธีการคำนวณจำนวนอิฐที่ต้องใช้ที่ฐานของพีระมิด

  • ขั้นที่ 2

    ทีนี้โจทย์ให้มาว่าในชั้นถัดไป จำนวนอิฐในแต่ละด้านจะลดลงไป 1 ดังนั้น

    ถ้าชั้นล่างสุดทั้งหมด 767 ก้อน
    ชั้นถัดมาจะลดลงเหลือ 765 เพราะตัดด้าน ซ้าย-ขวา ออกไปด้านละ 1 ก้อน ถัดไปอีกจะใช้แค่ 763
    และในแต่ละชั้นจะค่อยๆน้อยลงไปเรื่อยๆ จนเหลือแค่ 1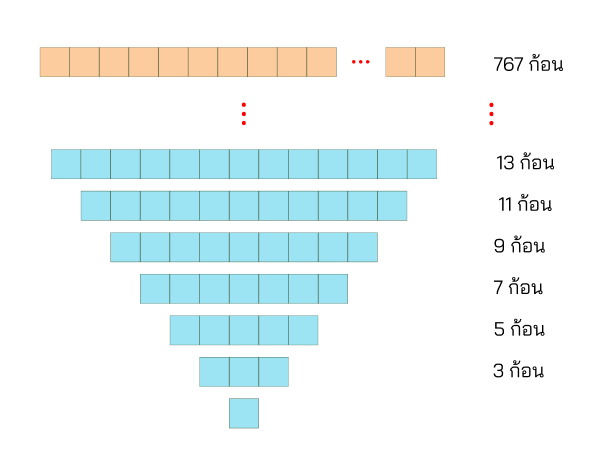

    ฐานพีระมิดที่ค่อยๆลดขนาดลงจนถึงยอดสุดที่มีแค่ก้อนเดียว ปริมาณอิฐจากชั้นล่างไปบนสุด

พื้นที่ของฐานแต่ละชั้นมีขนาดเท่ากับ กว้าง * ยาว อย่างเช่น ถ้าเป็นชั้นที่มีด้านละ 767 ก้อน ก็จะต้องใช้อิฐทั้งหมด 767 * 767 = 588,289 ก้อน

ทีนี้เราต้องคิดต่อไปจนถึงชั้นบนสุดหรือก็คือชั้นที่มีแค่ 1 ก้อน ดังนั้นคำตอบก็คือ

12+32+52+⋯+7652+76721^2+3^2+5^2+\dots+765^2+767^2

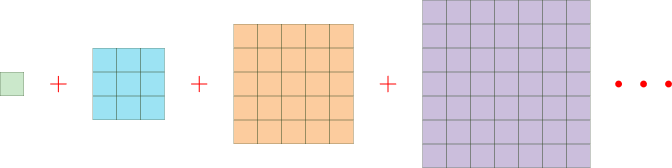ค่อยๆบวกทีละชั้นตั้งแต่ชั้นที่ 1 ที่มีแค่ 1 ถัดไปเป็นชั้นที่สองที่ใช้ 9 ก้อนไปเรื่อยๆ คำนวณจำนวนอิฐทั้งหมด

หรือแปลงเป็นผลรวมได้เป็น ∑i=1368(2∗i+1)2\sum_{i=1}^{368}{(2*i+1)^2}

  • ขั้นที่ 3 ถ้ารู้สูตรคำนวณเฉพาะเลยมันก็ง่ายเพราะว่าแค่แทนค่าลงไปเลยก็จบแล้ว

    ∑i=1368(2∗i+1)2=n(4n2−1)3\sum_{i=1}^{368}{(2*i+1)^2}=\frac{n(4n^2-1)}{3}

    แต่ถ้าไม่รู้ ก็ยังพอมีวิธีอื่นๆอยู่ เช่น กระจายสมการแล้วคิดแยกก็ได้

    ∑i=1n(2i+1)2=∑i=1n(4i2−4i+1)=∑i=1n4i2−∑i=1n4i+∑i=1n1=4∑i=1ni2−4∑i=1ni+∑i=1n1\begin{aligned} \sum_{i=1}^{n}{(2i+1)^2} & =\sum_{i=1}^{n}{(4i^2-4i+1)} \\& =\sum_{i=1}^{n}{4i^2} -\sum_{i=1}^{n}{4i}+\sum_{i=1}^{n}{1} \\& =4\sum_{i=1}^{n}{i^2}-4\sum_{i=1}^{n}{i}+\sum_{i=1}^{n}{1} \end{aligned}

    หรือจะคิดรวมไปถึง 767 แล้วค่อย ลบตัวที่เป็นเลขคู่ออกก็ได้เหมือนกัน

12+32+52+⋯+7652+7672=12+22+32+42+⋯+7652+7662+7672−22−42−⋯−7642−7662\begin{aligned}1^2+3^2+5^2+\dots+765^2+767^2 & = 1^2+2^2+3^2+4^2+\dots+765^2+766^2+767^2\\& -2^2-4^2-\dots-764^2-766^2 \end{aligned}

ซึ่งคำนวณได้เป็น

∑i=1767i2−∑i=1388(2i)2\sum_{i=1}^{767}{i^2}-\sum_{i=1}^{388}{(2i)^2}

สุดท้ายแล้ววิธีคิดมันมีเยอะมาก ขึ้นอยู่กับว่าเราจะมองปัญหาในรูปแบบไหน คิดได้ว่ายังไงมาแชร์กันได้ที่ลิ้งด้านล่างนะคร้าบ

โจทย์ชวนคิดเพิ่มเติม

ถ้าเปลี่ยนพีระมิดเป็นฐานสามเหลี่ยมแทน จะต้องใช้อิฐเท่าไหร่ ถ้าพีระมิดสูงทั้งหมด 1000 ชั้น?

พีระมิดสามเหลี่ยมที่ชั้นที่สองเป็นสามเหลี่ยมสามชั้นล้อมรอบสามเหลี่ยมตรงกลาง

ลิงก์

เรื่องเล่าชาวอัลกอ: Practical Algorithms
เรื่องเล่าชาวอัลกอ: Practical Algorithms Faviconhttps://www.facebook.com/share/p/RXjraWCFq3DMXneh/
 Genwit อัจฉริยะพันธุ์ใหม่
Genwit อัจฉริยะพันธุ์ใหม่ Faviconhttps://www.facebook.com/genwitofficial
แชร์หน่อยก๊าบ ⊹
  • คัดลอกแล้ว!
0