ปัญหา Birthday Paradox กับการสุ่มเพลง

เรื่องเล่าจากโพสต์ที่แล้ว:

วันก่อนนั่งคุยกับ roommate แล้วมี topic นึงน่าสนใจ เลยเอามาเล่าให้ฟัง เรื่องมันมีอยู่ว่ามันมีเครื่องเล่น MP3 อยู่ยี่ห้อนึงที่มันมีโหมดสุ่มเพลงขึ้นมาเล่น…

ประเด็นมีอยู่ว่า ระบบสุ่มของเครื่องเล่นตัวนี้มันสุ่มเพลงใหม่ทุกครั้งที่เล่นเพลงเก่าจบ แปลว่าเวลาสุ่มใหม่ก็มีโอกาสโดนเพลงเดิมอ่ะนะ

แล้วคนใน Reddit ช่องของ MP3 ตัวนี้ก็บ่นๆกันว่าเนี่ยใส่ไปตั้ง $100$ กว่าเพลง แต่เปิดสุ่มไปได้ $10$ กว่าๆเพลงก็เจอเพลงซ้ำแล้ว แถมซ้ำหลายรอบด้วย

ดูอีกปัญหาเล่นๆก่อนจะไปต่อ

แทนที่จะคิดเรื่องการสุ่มเพลง เดี๋ยวเล่าปัญหาใหม่อีกอันนึงให้ฟังก่อน:

มีห้องประชุมห้องนึง ที่มีคนอยู่ในห้องประมาณ 40 คน ถามว่ามีโอกาสที่คนในห้องมีคนเกิดวันตรงกันกี่เปอร์เซ็น?

ถ้าสมมติว่าปีนึงมีแค่ $365$ วัน คิดตาม common sense ปกติก็อาจจะคิดว่า โอกาสที่จะเกิดวันเดียวกันก็คงประมาณ $\frac{40}{365}$ ใช่มะ

จริงๆแล้วไม่ใช่เลย… การที่เราได้ $\frac{40}{365}$ มันมาจากการเปรียบเทียบคนในห้องประชุมที่มี $40$ คน กับจำนวนวันเกิดทั้งหมด $365$ วัน เมื่อเทียบกับคนๆเดียว อารมณ์แบบว่าถามว่าคนในห้องนั้นมีคนเกิดวันเดียวกันกับ ตัวเราเอง ไหม

ถ้ามองเป็นรูปภาพก็ลองคิดซะว่า แต่ละช่องเป็นวันเกิดที่เป็นไปได้ แล้วกากบาทคือมีคนเกิดวันนั้นไปแล้ว จะได้ว่า มันจะได้ว่ามีช่องอยู่ $365$ ช่องแล้วก็ $40$ ช่องโดนกากบาท

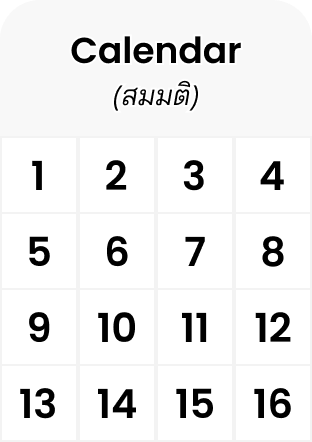ตารางขนาด 16 (4*4) ที่มีป้ายว่าปฎิทินแบบสมมติ รูปตารางขนาดวันเกิดแบบสมมติขนาด 16 (4*4)

เปลี่ยนจากที่มีคนอยู่ $40$ คนเป็น $4$ คนด้วยละกันเพื่อความง่าย

ถึงอย่างงั้นตอนเรามองที่ตาราง เราจะได้ว่าโอกาสจะซ้ำมันก็แค่ $\frac{1}{4}$ หรือ $\frac{4}{16}$ อยู่ดีใช่มะ แต่อย่างที่อธิบายไปตอนแรกคือ เราไม่ได้เทียบกับคนๆเดียวไง เราเทียบทุกคู่ที่อยู่ในห้องเลย

แล้วมันแปลว่าอะไรล่ะ? ถ้าเรามองในมุมมองของคนแรกที่อยู่ในห้อง (สมมติยังไม่มีใครเลยในห้องนอกจากคนแรก) แปลว่าตารางวันเกิด $16$ ช่องที่เรามียังไม่โดนใช้เลยสักช่อง หมายความว่าไม่ว่าคนแรกจะเกิดวันไหน ยังไงก็ไม่ซ้ำกับคนอื่นๆที่อยู่ในห้องแน่ๆ (แหงล่ะ ไม่มีใครในห้องหนิ 🤣)

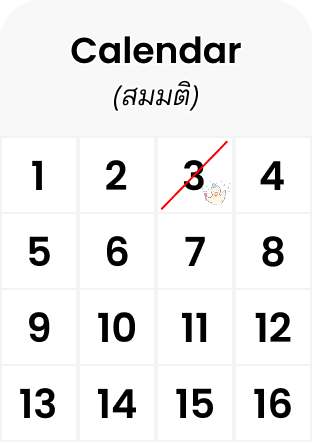ตารางขนาด 16 (4*4) ที่มีป้ายว่าปฎิทินแบบสมมติ และมีกากบาทที่ช่องหมายเลข 3 จาก 16 ปฏิทินแสดงโอกาสไม่ซ้ำหลังจากคนแรก

แล้วคนที่ถัดมาล่ะ? มันก็มีสองกรณีคือซ้ำกับคนแรกเลย (ซึ่งเป็นไปได้ยาก) หรือไม่ซ้ำกับคนแรกใช่มะ แต่การจะไม่ซ้ำกับคนแรก ก็แปลว่าคนที่สองมีวันเกิดอยู่ใน $15$ ช่องที่เหลือ หมายความว่ามีโอกาส $\frac{15}{16}$ ที่จะไม่ซ้ำ

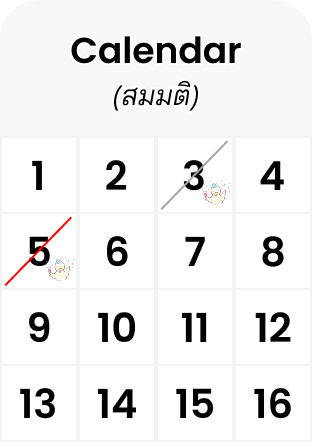ตารางขนาด 16 (4*4) ที่มีป้ายว่าปฎิทินแบบสมมติ และมีกากบาทที่ช่องหมายเลข 3 และ 5 จาก 16 ปฏิทินแสดงโอกาสไม่ซ้ำหลังจากคนที่สอง

คนที่สามล่ะ? ถ้าสมมติสองคนแรกไม่ซ้ำกัน เขาก็มีโอกาสซ้ำอยู่ $\frac{2}{16}$ และ โอกาสไม่ซ้ำ $\frac{14}{16}$

ซึ่งมันจะเป็นแบบนี้ไปเรื่อยๆนั่นแหละ คนที่สี่ก็มีโอกาส $\frac{13}{16}$ ที่จะไม่ซ้ำกับคนอื่นๆ ถ้าสมมติให้สามคนก่อนหน้าไม่ซ้ำกัน

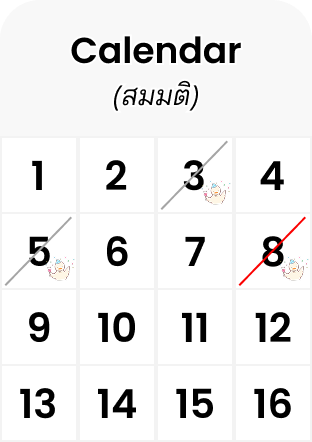ตารางขนาด 16 (4*4) ที่มีป้ายว่าปฎิทินแบบสมมติ และมีกากบาทที่ช่องหมายเลข 3,5 และ 8 จาก 16 ปฏิทินแสดงโอกาสไม่ซ้ำหลังจากคนที่สาม

แล้วมันแปลว่าอะไร… โอกาสที่จะมี $4$ คนในห้องแล้ววันเกิดไม่ซ้ำกันก็เป็น $\frac{16}{16} \times \frac{15}{16} \times \frac{14}{16} \times \frac{13}{16}$ จะได้ประมาณ $\frac{66}{100}$ $66\%$

แต่พอมีคนที่ 5 ที่โอกาสไม่ซ้ำอยู่ที่ $\frac{11}{16}$ ความน่าจะเป็นที่วันเกิดไม่ซ้ำมันตกมาเหลือราวๆ $50\%$ เลย แล้วถ้ามีคนที่ 6 ก็จะลงไปมากกว่านี้อีก

ซึ่งในกรณีวันเกิด $365$ วัน ใช้วิธีคิดแบบเดียวกัน จะได้ว่า แค่ $23$ คนก็ทำให้โอกาสไม่ซ้ำกันลงมาเหลือ แค่ประมาณ $50\%$ แล้ว

ถ้ามีสัก $40$ คน โอกาสที่จะไม่ซ้ำกันเลยจะลงมาเหลือแค่ $11\%$ หมายความว่ามีโอกาสประมาณ $89\%$ ที่มีจะคนเกิดวันซ้ำกัน

แวบแรกมันจะฟังดูขัด common sense ประมาณนึงเลย เขาก็เลยเรียกตัวนี้ว่า Birthday Paradox ถ้าอยากอ่านข้อมูลเพิ่มหาในเน็ตได้มีเยอะแยะ

กลับมาเรื่องเพลง

เหมือนนอกเรื่องมาเยอะ กลับมาเรื่องการสุ่มเพลงก่อน เรามีเพลงอยู่ $100$ เพลง แล้วต้องการสุ่ม $10$ ครั้งคิดเล่นๆว่าโอกาสที่จะสุ่มมาได้ ไม่ซ้ำกันเลยมีเท่าไหร่

ถ้าลองวาดเพลงแทนด้วยกล่องแล้วทำแบบเดิมก็จะได้ว่า… อ้าว มันคำถามเดียวกันกับเรื่องวันเกิดเลยนี่นา แค่ scale มันใหญ่ขึ้นเอง 😅

ถ้าอยากลองคิดเล่นๆว่ามีโอกาสเท่าไหร่ที่จะไม่มีเพลงซ้ำ ไปลองได้ฮะ (ใช้เครื่องคิดเลขก็ดีนะ) แต่มันจะได้สมการประมาณนี้:

\begin{aligned}\bar{p}(n,k) &= \prod_{i=0}^{k-1} \frac{n-i}{n} \\ &= (\frac{n}{n})\times (\frac{n-1}{n}) \times \cdots \times (\frac{n-k+1}{n})\end{aligned}

แต่ถ้าจะถามว่ามีโอกาสซ้ำกี่เปอร์เซ็น ก็เอาไปลบกับ $1$ :

1- \bar{p}(n,k)

ปล. สำหรับการสุ่มมา $10$ เพลงจาก $100$ จะมีโอกาสซ้ำประมาณ $37.1\%$

แอดเขียนโปรแกรมมาคำนวณทิ้งไว้อยู่เหมือนกัน: โปรแกรมคำนวณ Birthday_Paradox ที่เขียนเล่นๆ ไปอ่านเล่นได้ฮะ

ถามเล่นเรื่อยเปื่อย

แล้วถ้าสุ่ม $101$ ครั้ง จาก $100$ เพลงล่ะ?

แล้วมันสำคัญยังไง

เรื่องสุ่มเพลงอ่ะไม่ได้สำคัญหรอก มันสำคัญเพราะมันเกี่ยวกับเรื่องการทำ Hashing ถ้าไม่รู้ว่า Hashing คืออะไรไปอ่านโจทย์ข้อ Timerswitch โจทย์ข้อ Timerswitch จาก TOI13

หรือไม่ก็อ่านเรื่อง Rabin-Karp Algorithm ก็ได้เหมือนกัน เปรียบเทียบสตริงด้วย Rabin-Karp Algorithm

แต่หลักๆคือเราเห็นแล้วว่าการทำ Hash function ถ้า Range ของข้อมูลส่งออกมันเล็กมากๆ อย่างในกรณีวันเกิดมันก็มีแค่ $365$ เรา Hash ไม่เท่าไหร่ มันก็ collide แล้ว

ซึ่งตอนมัน collide เนี่ยน่ากลัวมาก เพราะมันทำให้เกิดปัญหาอย่างอื่นได้อีกเยอะ (ไว้หาโอกาสมาอธิบายทีหลังละกัน เดี๋ยวจะนอกเรื่องเยอะไป)