ปัญหาเหรียญปลอมเวอร์ชั่น 2 เหรียญ
ปกติถ้าอ่านโจทย์แนวนี้จะเจอแค่แบบเหรียญเดียวใช่ไหมล่ะ มันง่ายไป เอาไป 2 เหรียญเลยละกัน 555


โจทย์
มีเหรียญทั้งหมด 7 เหรียญ แต่ละเหรียญจะมีน้ำหนักเท่ากัน และมีทั้งหมด 2 เหรียญที่เป็นเหรียญปลอมที่เบากว่าปกติและหนักเท่ากัน
เราต้องการหาเหรียญปลอมทั้ง 2 เหรียญผ่านการชั่งกับตาชั่ง 2 แขน
ในการชั่งกับตาชั่ง 2 แขน จะวางกี่เหรียญทั้งสองฝั่งก็ได้ แต่จำนวนต้องเท่ากันทั้งสองฝั่ง
ถามว่าเราจะหาเหรียญปลอมผ่านการใช้ตาชั่ง 2 แขนไม่เกิน 3 ครั้งได้หรือไม่
วิเคราะห์โจทย์
ถ้าไปดูโจทย์เวอร์ชั่นทั่วๆไปอาจจะเจอแบบที่มีเหรียญหนัก/เบา แค่เหรียญเดียวซึ่งมันก็ทำง่ายๆแค่ แบ่งเป็นสามกองขนาดเท่าๆกัน แล้วก็ชั่งสองกองที่มีขนาดเท่ากัน แล้วก็หากองที่มีเหรียญเบากว่า แล้วก็ทำไปเรื่อยๆ… แค่พอมันมีสองเหรียญมันไม่ได้ง่ายขนาดนั้น 555
ปัญหานี้ค่อนข้างที่จะแก้ยากระดับนึง เพราะเราต้องหาทั้งสองเหรียญภายในการชั่งที่จำกัดมากๆ ซึ่งสมมติมีเหรียญปลอมแค่ 1 เหรียญจะใช้การชั่งแค่ 2 ครั้ง
ในโจทย์นี้ที่เราเลือกจำนวนเหรียญ 7 เหรียญเพราะเป็นจำนวนเหรียญที่มากที่สุดที่สามารถชั่ง 3 ครั้ง แล้วได้คำตอบอ่ะนะ เลยเอามาถามเล่นๆ
ทีนี้หลายๆ คนอาจจะเริ่มแก้ปัญหาด้วยการแบ่งเหรียญเป็น 2 ส่วนตรงๆ เลยเพื่อชั่งฝั่งซ้ายกับฝั่งขวา แล้วค่อยแบ่งเป็นอีก 2 ส่วนต่อตามผลลัพธ์การชั่งแต่ละครั้ง (ซึ่งกรณีนี้ก็มีวิธีแก้ได้เหมือนกัน แค่ต้องชั่งมากกว่า 3 ครั้ง)
แต่วิธีที่เรานำเสนอ จะแบ่งเหรียญเป็น 3 ส่วน ซึ่งก็เป็นหนึ่งในวิธีที่แก้ปัญหาได้ถ้ามีเหรียญมากกว่านี้ เพราะแบ่ง 2 ส่วนแล้วได้ข้อมูลไม่มากพอ
เริ่มแรกเลย เราจะพยายามแบ่งเหรียญให้เป็น 3 ส่วนคือ
- ส่วนที่อยู่ตาชั่งฝั่งซ้าย
- ส่วนที่อยู่ตาชั่งฝั่งขวา
- ส่วนที่อยู่ไม่ได้ชั่ง
เพื่อให้แบ่งแล้วคัดเหรียญออกได้มากที่สุดเท่าที่จะทำได้ เราจะแบ่งให้แต่ละส่วนขนาดต่างกันไม่เกิน 1 เหรียญ
 เอาเหรียญ 1 และ 2 วางบนตาชั่งสองแขนฝั่งซ้าย และเหรียญ 3 4 วางที่ฝั่งขวา
เอาเหรียญ 1 และ 2 วางบนตาชั่งสองแขนฝั่งซ้าย และเหรียญ 3 4 วางที่ฝั่งขวา
เพื่อความง่ายในการเรียกเราจะนิยามเพิ่มว่า คือน้ำหนักของเหรียญที่เลือก เมื่อ คือชุดหรือเซตของเหรียญที่เลือกมา
ในขั้นแรกก็จะแบ่งเป็นมี 2 เหรียญทั้งสองฝั่งตาชั่ง ขอเรียกว่าเป็นเหรียญหมายเลข 1 - 4 ละกัน
ชั่งครั้งที่ 1: เราจะเอาเหรียญที่ 1,2 ไว้ฝั่งซ้ายและ 3,4 ไว้ฝั่งขวา ทำให้ได้เป็น 3 เคส
- ฝั่งซ้ายเบากว่าฝั่งขวา ()
- ฝั่งซ้ายหนักกว่าฝั่งขวา ()
- ฝั่งซ้ายหนักเท่ากับฝั่งขวา ()
 รูปรวม 3 เคสที่สามารถเกิดขึ้นได้
รูปรวม 3 เคสที่สามารถเกิดขึ้นได้
กรณีที่ 1: ฝั่งซ้ายเบากว่าฝั่งขวา
 กรณีที่เหรียญ 3 และ 4 หนักกว่า
กรณีที่เหรียญ 3 และ 4 หนักกว่า
จะได้ว่าฝั่งซ้ายมีเหรียญปลอมอย่างน้อย 1 เหรียญแน่ๆ ทำให้เบากว่าฝั่งขวา และก็ชัวร์ว่าฝั่งขวาไม่มีเหรียญปลอมแน่ๆเหมือนกัน แต่ทีนี้เราจะหาว่ามีเหรียญปลอมในฝั่งซ้ายกี่เหรียญยังไง?
เหรียญที่โฟกัส: 1, 2, 5, 6, 7
ชั่งครั้งที่ 2: เราจะเอาเหรียญที่ 5 กับ 6 มาชั่งด้วยกันก่อน ก็จะได้เป็น 2 เคส
 การชั่งครั้งที่สอง
การชั่งครั้งที่สอง
-
ทั้งสองฝั่งหนักเท่ากัน ()
จะได้ว่าเหรียญที่ 5 กับ 6 เป็นเหรียญปกติทั้งคู่ ทำให้เหลือแค่เหรียญ 1, 2, 7 ที่มี 2 เหรียญที่เป็นเหรียญปลอม เราจะหาว่าเหรียญ 1 หรือ 2 ปลอมต่อ
เหรียญที่โฟกัส: 1, 2, 7
เราจะเอาเหรียญที่จริงแน่ๆ จากการชั่งครั้งที่ 1 มาชั่งใหม่อีกครั้ง
ชั่งครั้งที่ 3: เราจะเอาเหรียญที่ 1,3 ไว้ฝั่งซ้ายและ 2,4 ไว้ฝั่งขวา
 ชั่งครั้งที่ 3 เพื่อหาว่าเหรียญ 1 หรือ 2 ปลอม
ชั่งครั้งที่ 3 เพื่อหาว่าเหรียญ 1 หรือ 2 ปลอม ถ้าน้ำหนักเท่ากัน จะได้ว่าเหรียญ 1, 2 เป็นเหรียญปลอมทั้งคู่ ถ้าน้ำหนักฝั่งไหนที่เบากว่า ฝั่งนั้นมีเหรียญปลอม 1 เหรียญ และเหรียญปลอมอีก 1 เหรียญอยู่ที่เหรียญ 7
-
ทั้งสองฝั่งหนักไม่เท่ากัน ()
จะได้ว่าเหรียญที่ 5 หรือ 6 เป็นเหรียญปลอมโดยดูจากฝั่งที่เบากว่า หลังจากนั้นก็จะกลายเป็นว่าหาเหรียญปลอม 1 เหรียญจากไม่เหรียญหมายเลข 1 ก็ 2
ชั่งครั้งที่ 3: เราจะเอาเหรียญที่ปลอมที่ได้มาจากครั้งที่ 2 ไว้ฝั่งซ้ายและเหรียญหมายเลข 1 ไว้ฝั่งขวา
ถ้าน้ำหนักเท่ากัน จะได้ว่าเหรียญ 1 เป็นเหรียญปลอมด้วย ถ้าน้ำหนักไม่เท่ากันจะได้ว่าเหรียญ 2 เป็นเหรียญปลอม
กรณีที่ 2: ฝั่งซ้ายหนักกว่าฝั่งขวา
จะได้ว่าฝั่งขวามีเหรียญปลอมอย่างน้อย 1 เหรียญแน่ๆ ทำให้เบากว่าฝั่งซ้าย
 อีกเคสนึงหลังจากชั่งเหรียญ 1 - 4
อีกเคสนึงหลังจากชั่งเหรียญ 1 - 4
เหรียญที่โฟกัส: 3, 4, 5, 6, 7
ในการชั่งครั้งที่ 2 และ 3 จะทำในลักษณะคล้ายๆ กับกรณีที่ 1 แค่สลับฝั่งตาชั่ง
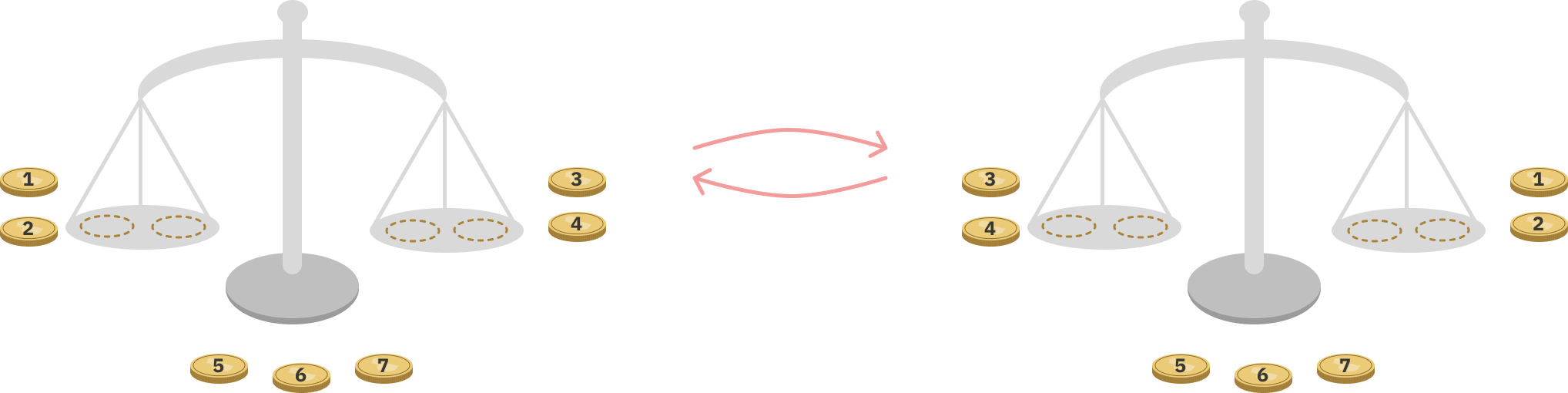 คิดแบบเดียวกันกับตอนที่ตาชั่งเอียงซ้ายได้เลย
คิดแบบเดียวกันกับตอนที่ตาชั่งเอียงซ้ายได้เลย
ก็คือสลับเหรียญ 1 2 กับ 3 4 หลังจากนั้นก็ทำเหมือนกับกรณีที่ 1 ได้เลย
กรณีที่ 3: ฝั่งซ้ายหนักเท่ากับฝั่งขวา
 กรณีตาชั่งสมดุลในการชั่งครั้งแรก
กรณีตาชั่งสมดุลในการชั่งครั้งแรก
จะได้ว่ามี 2 กรณีที่เป็นไปได้ คือทั้งสองฝั่งมีเหรียญปลอมฝั่งละ 1 เหรียญ หรือไม่ก็เหรียญปลอมอยู่ที่เหรียญ 5 - 7 ซึ่งเราจะแยกตรงนี้จากการชั่งครั้งที่ 2
เหรียญที่โฟกัส: 1, 2, 3, 4
ชั่งครั้งที่ 2: เราจะเอาเหรียญที่ 1,3 ไว้ฝั่งซ้ายและ 2,4 ไว้ฝั่งขวา
การชั่งในครั้งนี้จะต่างจากครั้งแรกเพราะจะทำให้เหรียญฝั่งนึงมีเหรียญปลอมไม่ 0 ก็ 2 เหรียญไปเลย ส่วนอีกข้างจะไม่มีเหรียญปลอมเลย ทำให้ได้เป็น 2 เคส
-
ทั้งสองฝั่งหนักไม่เท่ากัน ()
จะได้ว่าเหรียญในฝั่งที่เบากว่าจะเป็นเหรียญปลอมทั้งหมด ทำให้ไม่ต้องสนใจเหรียญ 5 - 7 และได้คำตอบเลย
-
ทั้งสองฝั่งหนักเท่ากัน ()
จะได้ว่าเหรียญปลอมทั้งสองเหรียญอยู่ที่เหรียญ 5 - 7 ทำให้จะใช้การชั่งครั้งที่ 3 มาดูว่าเหรียญ 5 - 7 เหรียญไหนปลอมบ้าง
เหรียญที่โฟกัส: 5, 6, 7
ชั่งครั้งที่ 3: เราจะเอาเหรียญที่ 5 ไว้ฝั่งซ้ายและ 6 ไว้ฝั่งขวา จะได้เป็น 2 เคส
ถ้าน้ำหนักเท่ากันคือเป็นเหรียญปลอมทั้งคู่เพราะมี 2 ใน 3 เหรียญที่เป็นเหรียญปลอม ถ้าน้ำหนักไม่เท่ากันคือฝั่งที่เบากว่าเป็นเหรียญปลอม และเหรียญ 7 เป็นเหรียญปลอมด้วย
สรุป
จริงๆ แล้วทั้ง 3 กรณีมีลักษณะที่เหมือนกันคือ เราสามารถสลับการชั่งครั้งที่ 2 และ 3 ได้ เพราะ
- การชั่งเหรียญ 1, 3 กับ 2, 4 เพื่อดูว่าในกลุ่มนี้มีเหรียญปลอมกี่เหรียญกันแน่
- การชั่งเหรียญ 5 กับ 6 เพื่อดูว่าเราควรใช้เหรียญไหนเป็นเหรียญปลอม จากการชั่งครั้งก่อนๆ และดูว่าเหลือเหรียญปลอมอีกกี่เหรียญ
ถ้าสนใจว่าเพิ่มจำนวนการชั่ง สามารถชั่งเหรียญได้กี่เหรียญและทำยังไง สามารถไปอ่านต่อกันได้เลย
ตัวอย่างการชั่งเหรียญมากกว่า 3 ครั้ง

