วิเคราะห์โจทย์จาก TOI18 ข้อ Constellation
โจทย์
มีแผนที่ท้องฟ้าขนาด อยู่ แต่ละพิกัดจะถูกระบุด้วย 2 สัญลักษณ์
.แทนพิกัดนั้นไม่มีดาว#แทนพิกัดนั้นมีดาวอยู่
เราต้องการหาจำนวนกลุ่มดาวทั้งหมดในแผนที่ท้องฟ้า โดยวิธีหากลุ่มดาวมีดังนี้
- เลือกจุดศูนย์กลางของกลุ่มดาวที่พิกัด โดยที่พิกัดนี้ต้องอยู่ในแผนที่
- เลือกดาวทั้งหมด ดวงที่ระยะห่างแบบ Manhattan(L1) จากจุดศูนย์กลางเท่ากัน ซึ่งระยะห่างตรงนี้จะยาวเท่าไหร่ก็ได้
โจทย์อยากทราบว่ามีวิธีการเลือกกลุ่มดาวได้ทั้งหมดกี่รูปแบบ โดยแสดงเศษจากหารจำนวนวิธีในการเลือกกลุ่มดาวด้วย
ข้อมูลนำเข้า
บรรทัดแรก ระบุจำนวนเต็ม จำนวนแถว จำนวนคอลัมน์ของแผนที่ดาว และขนาดของกลุ่มดาว (, )
บรรทัดต่อมา ระบุสายอักขระความยาว ที่ทุกตัวอักษร . หรือ # เท่านั้น
ข้อมูลส่งออก
มีทั้งหมด 1 บรรทัด แสดงจำนวนเต็ม จำนวน แทนค่าวิธีการเลือกกลุ่มดาว โดยแสดงเศษจากการหารด้วย
ตัวอย่างข้อมูลนำเข้าและข้อมูลส่งออก
| Input | Output |
|---|---|
| 3 2 2 #. .# #. | 8 |
| 3 3 2 #.. .#. #.. | 11 |
| 5 4 3 .#.# #.#. .#.# #.#. .#.# | 240 |
| 20 20 19 #################### #################### #################### #################### #################### #################### #################### #################### #################### #################### #################### #################### #################### #################### #################### #################### #################### #################### #################### #################### | 199545 |
วิเคราะห์โจทย์
ก่อนอื่นเลย เราจะมาดูก่อนว่าจะเลือกกลุ่มดาวยังไงดี
เลือกจากจุดศูนย์กลางก่อน
แน่นอนแหละว่า ถ้าไม่มีจุดศูนย์กลางเราก็จะไม่สามารถทำอะไรต่อจากเดิมได้ซักเท่าไหร่ ซึ่งการจะกำหนดจุดศูนย์กลางทำได้ค่อนข้างง่ายเพราะก็แค่ไล่ลูปทุกพิกัดที่เป็นไปได้ก็แค่นั้น แต่ปัญหาจะเริ่มเกิดขึ้นในขั้นตอนถัดๆ มาซะมากกว่า
ปัญหา 1: เลือกดาวให้กลุ่มดาว
หลังจากเลือกจุดศูนย์กลางเสร็จแล้ว เรียกว่าเป็นจุด ละกัน ทีนี้เดี๋ยวเราจะต้องไปหาให้ได้ว่าดาวที่จะต้องเลือกมาทั้ง ดวงที่ระยะห่างจาก เท่ากันทั้งหมดมันมีกี่แบบ
ด้วยความที่โจทย์ไม่ได้ลิมิตระยะห่างของดาว เราก็แค่ต้องไล่ลูประยะจากระยะห่าง 1 ไปจนถึงขอบตารางเพื่อจะได้คิดทุกรูปแบบ
 รูปแสดงระยะห่างของดาวเทียบกับจุดศูนย์กลาง
รูปแสดงระยะห่างของดาวเทียบกับจุดศูนย์กลาง
แต่ๆๆๆ คำถามต่อมาคือ ถึงรู้แล้วว่ามีกี่ดวงในระยะ แล้วเราจะเลือกจำนวนรูปแบบของดาวที่เป็นไปได้ยังไงล่ะ
ปัญหา 2: แล้วเลือกได้กี่แบบล่ะ?
เราจะมาลองดูอีกปัญหานึงหลังจากเรื่องการหาดาวคือ ถ้าเรารู้แล้วว่ามีดาวที่เลือกได้ทั้งหมด ดวง แล้วต้องการจะเลือกมาเพียง ดวง จะทำยังไงดี?
เพื่อความง่าย เราจะลองเอาดาวมาเรียงเป็นเส้นตรง แล้วเลือกดาวในแต่ละตำแหน่งดู
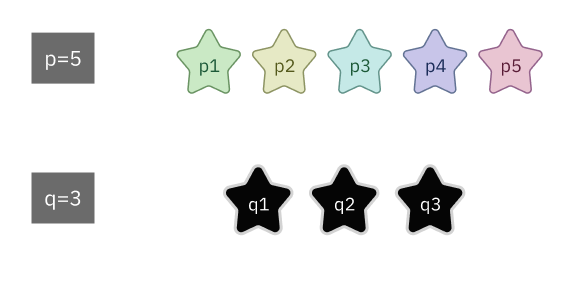 มีดาวให้เลือกได้ 5 ดวง และต้องการเลือกมา 3 ดวง
มีดาวให้เลือกได้ 5 ดวง และต้องการเลือกมา 3 ดวง
ตำแหน่งที่ 1 เราจะเลือกดาวได้ทั้งหมด รูปแบบ
ตำแหน่งที่ 2 เราจะเลือกดาวได้ทั้งหมด รูปแบบ
ตำแหน่งที่ 3 เราจะเลือกดาวได้ทั้งหมด รูปแบบ
ถ้าคิดต่อไปจนถึง
ตำแหน่งที่ เราจะเลือกดาวได้ทั้งหมด รูปแบบ
ซึ่งรวมๆแล้วแปลว่าทำได้ทั้งหมด แบบเมื่อ คือผลคูณตั้งแต่ 1 ถึง
แต่การทำแบบนี้จะเห็นได้ว่าลำดับการเลือกในแต่ละตำแหน่งส่งผลต่อจำนวนรูปแบบที่เกิดขึ้นได้ (permutation) ซึ่งเราไม่ต้องการแบบนั้น
 ลำดับการเลือกดาวมีผลกับจำนวนรูปแบบที่เกิดขึ้นได้ ซึ่งเราไม่สนใจลำดับในการเลือกดาว
ลำดับการเลือกดาวมีผลกับจำนวนรูปแบบที่เกิดขึ้นได้ ซึ่งเราไม่สนใจลำดับในการเลือกดาว
เราก็เลยต้องหาต่อว่าการสลับที่จากดาวที่เลือกมามีกี่รูปแบบ ในที่นี้เราเลือกดาวมา ดวง ก็เลยสลับได้ แบบ (เลือก ช่องจาก ช่องโดยคิดเรื่องลำดับ)
ทีนี้เราจะเอาจำนวนรูปแบบทั้งหมด () มาหารด้วยจำนวนลำดับจากการ permutation ของในกลุ่มเดียวกันทิ้ง () ทำให้สุดท้ายเหลือจำนวนรูปแบบเป็น (ในทางคณิตศาสตร์จะเรียกว่า Combination)
เราสามารถเรียก Combination ตรงส่วนนี้ว่า เป็นการเลือกดาว ดวงจากดาว ดวง ซึ่งในส่วนนี้เราสามารถคำนวณเอาไว้แล้วเก็บค่าลงในอาเรย์เอาไว้เพื่อใช้ต่อทีหลังได้ จะได้ไม่ต้องคำนวณใหม่เรื่อยๆ
แต่ทีนี้เราจะคำนวณ ให้เร็วๆได้ยังไง?
Preprocess ค่าวิธีเลือก
การหาค่า สามารถทำได้จากการใช้สามเหลี่ยม Pascal ได้เลย ซึ่งก็คือ
เนื่องจากว่าจำนวนดาวมากสุดที่เป็นไปได้ในการเลือกมีอยู่ประมาณ ดวง และเราก็เลือกแค่ ดวงอยู่แล้ว
ทำให้เราไม่ต้องคิดทั้งสามเหลี่ยม Pascal ทั้งอัน และคำนวณ preprocess แค่ถึง ซึ่งทำได้ใน
สามเหลี่ยม Pascal
ถ้าสนใจว่าค่าจากสามเหลี่ยม Pascal มายังไงก็สามารถอ่านต่อได้เลย หรือจะข้ามไปส่วนต่อไปเพื่อไปใช้ดูว่าเอาสามเหลี่ยม Pascal ไปใช้ในโจทย์ยังไงดี
ทีนี้เราจะมาโฟกัสที่ปัญหานึงกัน ปัญหาที่ว่าคือเราต้องการเลือกของจากทั้งหมด ชิ้นมาจำนวน ชิ้นโดยไม่สนใจลำดับในการหยิบ ซึ่งจะมาคิดแยกเป็น 2 วิธีกัน
- ใช้นิยามการเลือกตรงๆ ไปเลย ก็จะได้ว่ามีค่าเป็น
- คิดว่าการเลือกที่ว่านั้นมีความเป็นไปได้ 2 รูปแบบที่ครอบคลุมตามการเลือกเริ่มต้น แล้วมารวมกัน
- มีของทั้งหมด ชิ้นแล้วเลือก ชิ้นไปแล้วก่อนหน้านั้น ทำให้ชิ้นที่ ต้องเลือกแน่ๆ ()
- มีของทั้งหมด ชิ้นแล้วเลือกครบ ชิ้นไปแล้วก่อนหน้านั้น ทำให้ชิ้นที่ ยังไงก็ไม่เลือกแน่ๆ ()
ซึ่งวิธีพิสูจน์แบบนี้ก็มีชื่อเรียกเฉพาะก็คือ Combinatorial Proof ถ้าสนใจก็ไปอ่านต่อกันได้ 😁
กลับมาที่การหาจำนวนดาวในระยะต่างๆ
หลังจากได้วิธีการคิดจำนวนวิธีการเลือกดาวแล้ว ทีนี้เราจะกลับมาหาว่าในแต่ละระยะมีดาวกี่ดวงกันแน่
ทางที่ง่ายที่สุดก็คือในทุกๆ จุดศูนย์กลาง เราสามารถไล่หาทั้งตารางเทียบกับ ที่กำลังดูอยู่ว่า ดาวแต่ละพิกัดมันห่างจากจุดศูนย์กลางเท่าไหร่ แล้วก็เก็บว่าแต่ละระยะมีดาวทั้งหมดกี่ดวง ซึ่งในการไล่ตรวจทั้งตารางจะใช้เวลา เพราะทั้งตารางมีขนาด
แล้วเราก็แค่ต้องทำแบบนี้ไปเรื่อยๆทุกจุดศูนย์กลางเอง ซึ่งก็มีอีก จุด ดังนั้นแค่จะมองหาว่ามีดาวกี่ดวงอยู่รอบๆก็ใช้ไปแล้ว
ต่อมาตอนเราจะคำนวณจำนวนวิธี ก็จะไปดูในทุกระยะจากจุดศูนย์กลางว่า แต่ละระยะเลือกนั้นเป็นไปได้กี่รูปแบบ ทำให้เรียกใช้ค่า ได้ เมื่อ คือจำนวนดาวที่ระยะห่าง จากพิกัด เพราะเราต้องการเลือกดาวมาแค่ ดวง จาก ดวงทั้งหมดในระยะนั้นๆ
ซึ่งระยะทางที่ว่ามีค่ามากที่สุดได้ถึง ฃดังนั้นเราจะต้องคำนวณค่า ในทุกระยะที่เป็นไปได้ ซึ่งก็จะใช้เวลา ส่วนค่าที่ต้องคำนวณก็ไปดึงเอามาจากอาเรย์ที่เก็บไว้จากที่คิดเมื่อในสเต็ปที่แล้วได้เลย
ละก็เหมือนเดิมที่ก็ต้องไปคิดแบบนี้ในทุกๆจุดศูนย์กลาง ก็เลยใช้เวลาในพาร์ทนี้เป็น
ทีนี้เราจะมาค่อยๆดูว่าจะ optimize วิธีคิดจากส่วนไหนกันต่อได้บ้าง เพื่อให้ผ่านโจทย์ข้อนี้ไปได้ 😅
- การไล่ลูปหาจุดศูนย์กลาง: ใช้เวลา ซึ่งก็น่าจะดีที่สุดแล้ว เพราะไม่มีวิธีคิดรวบทีเดียวหลายๆจุด เนื่องจากแต่ละจุดมีจำนวนดาวรอบๆไม่เท่ากัน
- หาจำนวนวิธีเลือกดาวในแต่ละระยะ: ก็เรียกใช้จากที่ preprocess จากสามเหลี่ยม Pascal มาได้เลย ซึ่งเรียกใน และ preprocess ใน ตอนแรกสุด ซึ่งก็ไม่ได้แย่อีก
- นับจำนวนดาวที่อยู่ในแต่ละระยะ: ใช้เวลาคำนวณระยะทุกช่องในตาราง เพื่อให้ได้ทุกระยะต่อ 1 จุดศูนย์กลาง ซึ่งดูแย่ที่สุด ทำให้เราจะมา optimize ต่อในส่วนนี้
หาจำนวนดาวแบบเร็วๆ
จากการเลือกดาวในแต่ละระยะจะสังเกตได้ว่า ถ้าเรา fix ระยะเป็นค่าๆนึง ระยะนั้นจะประกอบด้วยเส้นทแยงมุมทั้งหมด 4 เส้นมารวมกัน ทำให้เราจะใช้ประโยชน์จากข้อสังเกตนี้กัน
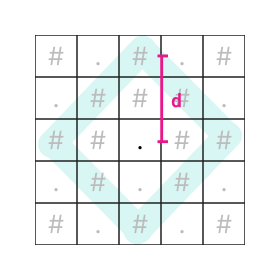 เส้นรอบจุดศูนย์กลางที่เราสนใจ ในระยะห่าง d
เส้นรอบจุดศูนย์กลางที่เราสนใจ ในระยะห่าง d
มองเพิ่มอีกนึดนึงเราจะเห็นว่าเส้นทแยงมุมทั้ง 4 เส้นเนี่ย จริงๆมันมีแค่ 2 แนวเอง คือทแยงจากบนซ้ายไปล่างขวา กับบนขวาไปล่างซ้าย
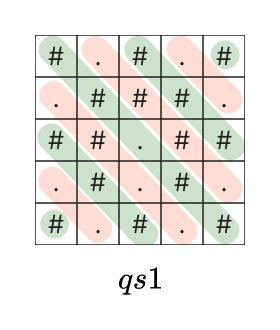 เส้นทแยงจากบนซ้ายไปล่างขวา
เส้นทแยงจากบนซ้ายไปล่างขวา
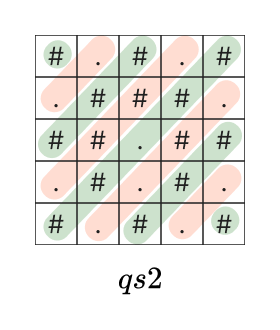 เส้นทแยงจากบนขวาไปล่างซ้าย
เส้นทแยงจากบนขวาไปล่างซ้าย
เราจะทำการเก็บผลรวมของดาวในตามแนวทแยง (Quicksum) ทั้งสองแนวกันก่อน ซึ่งก็จะสร้างอาเรย์ 2 มิติเก็บผลรวมมาทั้งหมด 2 อาเรย์ สมมติว่าเป็น และให้จำนวนดาวที่พิกัด คือ (มีค่าเป็น 0 หรือ 1)
- มุมจากซ้ายบนไปขวาล่าง: สำหรับพิกัด ใดๆ เราจะเก็บค่า เป็น
- มุมจากขวาบนไปซ้ายล่าง: สำหรับพิกัด ใดๆ เราจะเก็บค่า เป็น
ทีนี้พอจะหาว่าในเส้นทแยงมุมว่ามีกี่จุดก็แค่เอาผลรวมของเส้นทแยงมุมมาหักลบกันเพื่อดูว่าในช่วงๆนึงของเส้นกี่จุด เท่านี้ก็สามารถหาได้แล้วว่าในระยะที่เราต้องการหาจะมีดาวกี่ดวง
รวมทุกอย่างเข้าด้วยกัน
ทีนี้เราก็จะใช้ค่าที่ preprocess ได้ มาคู่กับลูปเรื่องระยะ ทำให้ในแต่ละระยะเราแค่เรียกผลรวมแนวทแยงทั้ง 4 ด้านมาใช้ได้โดยใช้เวลาใน ซึ่งลดเวลาจาก เหลือแค่ ต่อ 1 จุดศูนย์กลาง เพราะเหลือแค่ต้องลูปเรื่องระยะแทน
สุดท้ายทำให้หาค่าจำนวนกลุ่มดาวได้ภายใน ซึ่งก็ทำให้ผ่านข้อนี้ได้แล้ว 🎉