โจทย์ข้อ Kay and Snowflake จาก Codeforces
มีโจทย์กราฟสวยๆมาฝากกันอีกแล้ว คราวนี้เราจะมาเรียนรู้วิธีการหาจุดกึ่งกลาง(Centroid) ว่าเป็นยังไงกัน


โจทย์ (ฉบับย่อ)
ความยาก ★★★★★
มีกราฟที่เป็น tree อยู่ต้นนึง ต้นไม้ต้นนี้มีโหนดทั้งหมด โหนด เราอยากรู้ว่าจุดกึ่งกลาง(Centroid) ของต้นไม้นี้อยู่ที่โหนดไหน
โดยโจทย์ข้อนี้มีคำถามทั้งหมด คำถาม แต่ละคำถามจะถามว่าถ้าเราพิจารณาแค่ Subtree ของบางโหนดแล้ว Centroid ของ Subtree นั้นจะอยู่ที่ไหน
Centroid มีคำนิยามว่า ถ้าตัดโหนดนี้ออกไปแล้ว Component ที่เหลือของต้นไม้นี้จะมีขนาดไม่มากกว่าครึ่งหนึ่งของขนาดต้นไม้
Subtree ของโหนด มีคำนิยามว่า เป็นส่วนหนึ่งของ tree หลักโดยที่จะรวมโหนด ,โหนดลูกของ และทุกตัวที่เป็นโหนดลูกลงไปเรื่อยๆ
ข้อมูลนำเข้า
บรรทัดแรก ระบุจำนวนเต็ม () แทนขนาดของต้นไม้ และจำนวนคำถามที่จะถาม
บรรทัดต่อมา ระบุจำนวนเต็มทั้งหมด ตัว แทนเลขโหนดที่เป็นโหนดพ่อ (Parent Node) ของโหนด ถึง ()
บรรทัดต่อมา ระบุจำนวนเต็ม แทนเลขโหนดของ subtree ที่ต้องการจะถาม
ข้อมูลส่งออก
มี บรรทัด แต่ละบรรทัดแสดงเลข index ของโหนดที่เป็น Centroid ของ Subtree นั้นๆ โดยที่ทุกๆ Tree และ Subtree จะรับประกันว่ามี Centroid อย่างน้อย 1 โหนดเสมอ ถ้ามีมากกว่า 1 โหนด ตอบโหนดไหนก็ได้
ตัวอย่างข้อมูลนำเข้าและข้อมูลส่งออก
| Input | Output |
|---|---|
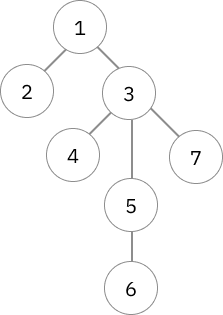
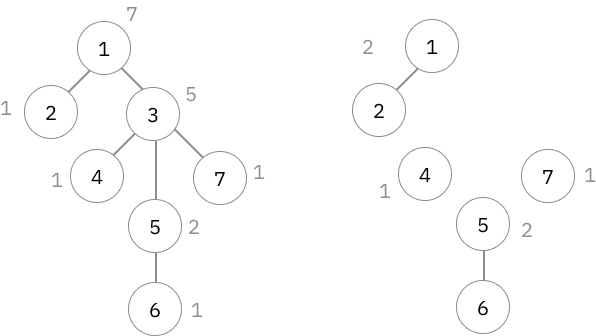
| 7 4 1 1 3 3 5 3 1 2 3 5 | 3 2 3 6 |
คำอธิบายข้อมูลนำเข้าและข้อมูลส่งออก:
- ในคำถามแรกเป็นการหาจุดกึ่งกลางของต้นไม้ทั้งต้นเลย และเมื่อเราลบโหนด 3 ออกไป ต้นไม้จะกลายเป็น 4 component ย่อยที่มีขนาด 1, 1, 2, 2
- Subtree ของโหนด 2 คือโหนด 2 เอง ซึ่งจะได้ว่า Centroid ของ Subtree นี้คือ 2
- Subtree ของโหนด 3 จะมีโหนด 3, 4, 5, 6, 7 ซึ่งจะได้ว่า Centroid ของ Subtree นี้คือ 3
- Subtree ของโหนด 5 จะมีโหนด 5 และ 6 ที่มีขนาดแค่ 2 ซึ่งจะได้ว่า Centroid ของ Subtree นี้คือ 5 หรือ 6 ก็ได้
 กราฟจากตัวอย่าง
กราฟจากตัวอย่าง
วิเคราะห์โจทย์
ก่อนอื่นเลย เราจะมาดูนิยามของคำที่เกี่ยวข้องกันก่อน
จุดกึ่งกลาง (Centroid)
Centroid ของ tree เป็นโหนดที่เมื่อตัดจุดนั้นออกไปแล้วจะได้เป็น component ย่อยๆ ที่ขนาดของแต่ละ component จะไม่เกินครึ่งหนึ่งของขนาดต้นไม้ ซึ่งสำหรับทุก tree จะรับประกันว่ามีจุดที่เป็น centroid อยู่อย่างน้อย 1 โหนดและมีไม่เกิน 2 โหนด และสองโหนดนั้นจะเป็นโหนดที่ติดกันด้วย
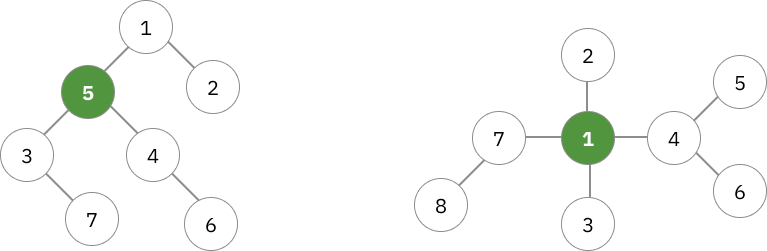 ตัวอย่าง Centroid ในกราฟ
ตัวอย่าง Centroid ในกราฟ
 หลังจากตัด Centroid ออกแล้ว
หลังจากตัด Centroid ออกแล้ว
ซึ่งถ้า tree มีขนาดเล็กมากๆ เช่น 1 หรือ 2 โหนด โหนดๆนั้นก็จะเป็น centroid ของต้นไม้นั้นเลย
 กราฟที่มีขนาด 1 และ 2
กราฟที่มีขนาด 1 และ 2
วิธีการหา Centroid
ในการหา centroid ของ tree ตามปกติแล้วจะคิดได้โดยการดูทุกโหนดเลย แล้วก็ทดลองแบ่งต้นไม้ออกมาดูและเช็กขนาดของทุก component ที่แบ่งออกมาได้ว่าเข้ากับเงื่อนไขของ centroid ไหม ซึ่งถ้าทำวิธีตามปกติก็จะต้องไล่ทุกโหนด(อีกตามเคย 😐) แล้วดูว่าแต่ละตัวอยู่ component ไหน ซึ่งรวมๆแล้วจะใช้เวลา ในการแบ่งและตรวจสอบ สำหรับแค่ 1 โหนด ทำให้การแบ่งทุกโหนดจะใช้เวลา เพื่อจะให้หา centroid ได้
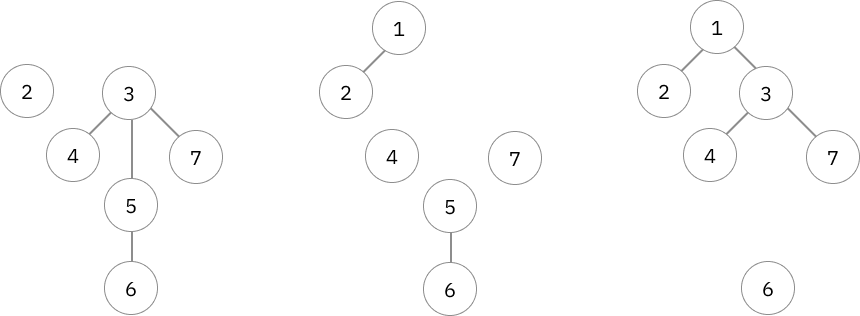 ลองตัดดูทีละโหนดไปเรื่อยๆ
ลองตัดดูทีละโหนดไปเรื่อยๆ
ทีนี้แค่การหา centroid ของ tree 1 ต้นใช้เวลานานมากๆ (แค่ต้นเดียวก็ไม่ทันเวลาแล้ว 😅) เราจึงจะสร้าง array มาตัวนึงเพื่อเก็บว่า subtree ของโหนดแต่ละตัวมีขนาดเท่าไหร่ ซึ่งทำให้พอเวลาดูโหนดใดๆ ที่จะตัดในกราฟ(สมมติว่าเป็น ) เราจะดูแค่โหนดลูกของ ทั้งหมดว่าขนาดไม่เกินครึ่งหนึ่งของขนาดต้นไม้ และขนาดของ component ที่เป็น parent ของ ก็ได้แล้ว ซึ่งหาได้ด้วยการนำขนาดของ tree มาลบด้วยขนาดของ subtree
ถ้ารู้ขนาดต้นไม้แล้วการจะหาขนาดของ component ที่เป็น parent ของโหนด ก็แค่
เมื่อเราทำแบบนี้แล้วเราจะได้ว่าเราสามารถตอบได้ในเวลา ว่าแต่ละ component มีขนาดเท่าไหร่เมื่อตัดโหนดออกไป 1 ตัว ซึ่งหลังจากตัดเสร็จก็แค่เช็กตอนสุดท้ายว่าขนาดไม่เกินครึ่งหนึ่งของขนาดต้นไม้มั้ย ถ้าใช่ ก็ตอบโหนดนั้นไปได้เลย ถ้าไม่ใช่ก็ดูโหนดถัดไป ทำให้ลดเวลาเหลือแค่ ในการหา centroid ของ tree 1 ต้น
แต่ในโจทย์ก็มีโอกาสถามทุกโหนด แบบนี้ก็มีโอกาสทำไม่ทันหนิ
การหา Centroid ของทุก subtree
ทีนี้เราจะทำการหา centroid ของแต่ละ subtree โดยใช้ข้อมูลโหนดลูกของ subtree นั้นมาเป็นข้อมูลมาคิดด้วย
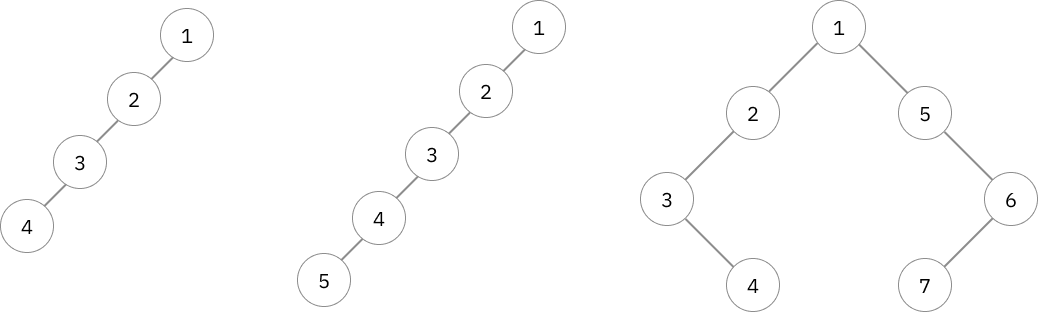
ก่อนอื่นเลยลองมองเคสตัวอย่างที่คิดง่ายๆดูก่อน เช่น ถ้าเราเจอว่า ต้นไม้ที่เราดูอยู่มีแค่ 1 หรือ 2 โหนด เราสามารถตอบได้ทันทีเลยว่า centroid ของ subtree คือโหนดนั้นเองนั่นแหละ
 กราฟที่มีขนาด 1 และ 2
กราฟที่มีขนาด 1 และ 2
ซึ่งมันก็คิดได้ไม่ยากเพราะมันก็ค่อนข้างตรงตัว ทีนี้ลองค่อยๆคิดว่าถ้าลองขยับให้มันมีขนาดอื่นๆล่ะ?
 กราฟที่มีขนาดใหญ่ขึ้น
กราฟที่มีขนาดใหญ่ขึ้น
ต้นไม้ทั้งหมดนี้มี centroid อยู่ทุกต้นแหละ แต่คำถามคือ แล้วเราจะคำนวณมันยังไงดีล่ะ?
จริงๆแล้วเราพอรู้ข้อมูลบางอย่างจะก่อนหน้านี้แหละ แล้วเราสามารถใช้ข้อมูลเหล่านี้ในการเอามาสร้างคำตอบได้
ตัวอย่างการหา centroid ใน subtree
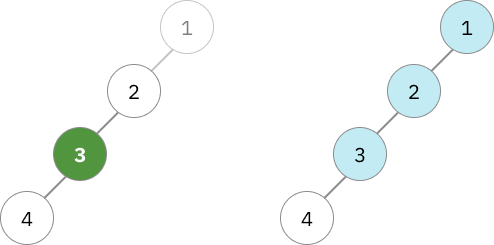
อย่างในรูปแรกถ้าเราดูแค่ subtree ที่มีโหนด 2 เป็น root ซึ่งก็คือมีแค่โหนด 2, 3 และ 4 ซึ่งเรารู้ว่า centroid เป็นตัวที่ 3 แน่ๆแหละ (มันชัดอ่ะนะ)
 กลับมาที่กราฟเดิม
กลับมาที่กราฟเดิม
ทีนี้พอเพิ่มโหนด 1 เข้ามา Centroid ของ tree ใหม่มันจะมีความเป็นไปได้อยู่ 3 กรณี:
- เป็นโหนดเดิมของต้นไม้เก่า
- เป็นโหนดที่อยู่ระหว่าง centroid เก่า กับ root ที่เพิ่งเพิ่มเข้ามาใหม่
- เป็นโหนดที่เพิ่งเข้ามาใหม่นั่นแหละ
สังเกตว่า centroid ไม่มีทางเป็นโหนดที่อยู่ต่ำกว่า centroid เก่าแน่ๆ เพราะว่ามันมีแต่จะทำให้ component หลังจากตัดมันใหญ่ขึ้นซึ่งขัดกับนิยาม centroid เลย
หลังจากเพิ่มโหนด 1 เข้ามาในตัวอย่างแรกด้วย เราจะได้ว่า 3 ยังเป็น centroid ได้อยู่ โดยใช้วิธีตรวจสอบด้วยขนาดของต้นไม้เหมือนวิธี ที่อธิบายไว้ตอนแรกได้เลย ซึ่งแปลว่าเราก็ตอบ 3 ได้เลย
ตัวอย่างของเคสที่ 2
 ถ้ากราฟขนาด 5 ล่ะ?
ถ้ากราฟขนาด 5 ล่ะ?
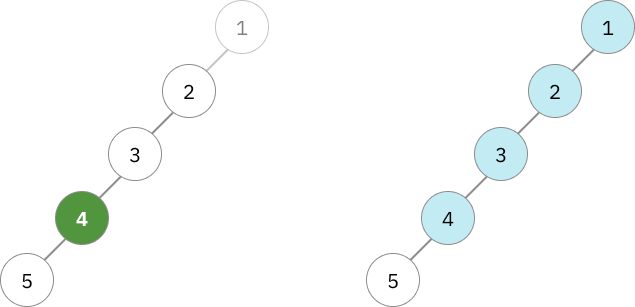
ถ้าพิจารณาแค่ subtree ที่มี 1 เป็น root เราจะได้ว่าโหนด 3 และ 4 เป็น centroid ในที่นี้ขอใช้ว่าโหนด 4 เป็น centroid เพื่อจะใช้อธิบายได้ง่ายขึ้น
ในเคสนี้เมื่อเพิ่มโหนด 1 เข้ามาแล้ว โหนดที่ 4 ไม่ได้เป็น centroid แล้ว ทำให้เราต้องหาโหนดใหม่มาแทน จากข้อสังเกตก่อนหน้านี้ว่าตัวที่อยู่ลึกกว่าไม่มีทางเป็น centroid แน่ๆ แปลว่าเราต้องค่อยๆไล่ตรวจสอบโหนดที่อยู่สูงขึ้นไปเรื่อยๆ
ซึ่งเราจะขยับโหนด 4 ขึ้นไปทางโหนดพ่อที่เพิ่งถูกเพิ่มลง tree ไปเรื่อยๆ (ซึ่งก็คือ 3 ก่อน แล้วตามด้วย 2 จนถึง 1) ถ้าโหนดไหนที่ดูอยู่ที่เป็น centroid ได้แล้ว เราก็จะเอาโหนดนั้นมาตอบเป็น centroid ของ subtree ไปเลย
จากตัวอย่างเราตรวจสอบขึ้นไปถึงแค่ โหนด 3 ก็พอแล้วเพราะมันเป็น centroid แล้ว (คำนวณขนาดจากวิธีก่อนหน้านี้ที่เก็บขนาดต้นไม้ไว้)
ตัวอย่างของเคสที่ 3
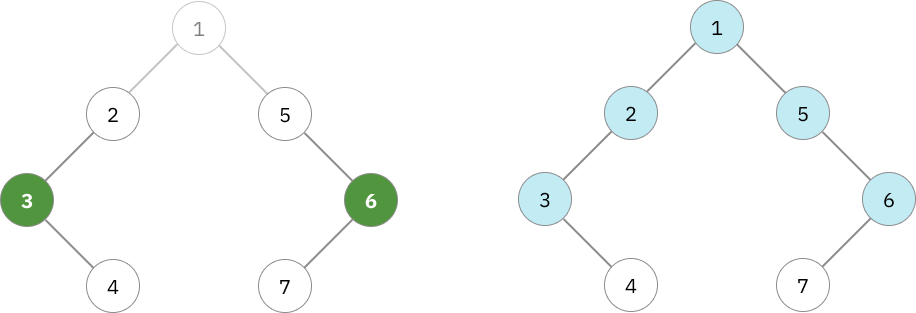 กราฟที่มีขนาดใหญ่ขึ้น
กราฟที่มีขนาดใหญ่ขึ้น
เมื่อเราเพิ่มโหนด 1 เข้ามาด้วย เราจะต้องดูจากทั้ง 2 subtree ที่เป็นลูกของ 1 ซึ่งก็จะเช็กเหมือนกรณีก่อนหน้านี้ แต่ต้องเช็กสำหรับลูกทุกตัว
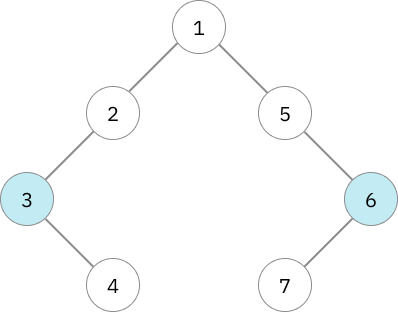 เริ่มจากการตรวจสอบโหนดที่เคยเป็น centroid ก่อน
เริ่มจากการตรวจสอบโหนดที่เคยเป็น centroid ก่อน
จากตัวอย่างเราจะเริ่มจากการตรวจสอบโหนดที่เคยเป็น centroid ก่อน ซึ่งในกรณีนี้คือ 3 และ 6 จากการที่ดูจากขนาดของ subtree หลังจากตัดโหนด 3 หรือ 6 ไป จะได้ว่า subtree ที่เหลือ ไม่ได้เข้าเงื่อนไขการเป็น centroid ทำให้ต้องไปเช็กโหนดอื่นๆแทน
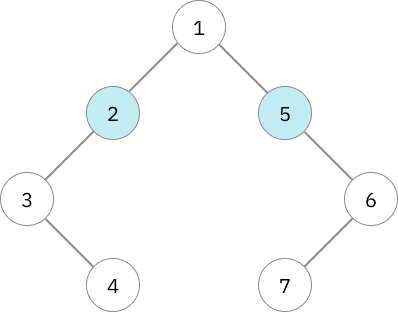 เริ่มจากการตรวจสอบโหนดพ่อของโหนดที่เคยเป็น centroid
เริ่มจากการตรวจสอบโหนดพ่อของโหนดที่เคยเป็น centroid
ในเมื่อโหนด centroid เก่าจากทั้ง 2 subtree นั้นไม่สามารถใช้ได้แล้ว centroid ใหม่ก็จะอยู่ตรงไหนสักที่ระหว่าง centroid เก่ากับโหนดที่เพิ่งเพิ่มเข้ามา ดังนั้นเราก็จะต้องตรวจสอบโหนดที่อยู่สูงขึ้นไปบนกราฟเรื่อยๆ อย่างในกรณีนี้ก็จะเป็นโหนด 2 และ 5 ซึ่งก็ยังไม่ใช่ centroid อยู่ดี
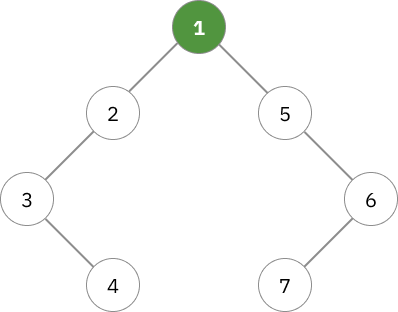 ตัวอื่นๆที่ตรวจสอบไปแล้วไม่สามารถใช้ได้เลย
ตัวอื่นๆที่ตรวจสอบไปแล้วไม่สามารถใช้ได้เลย
ถ้าเช็กเสร็จแล้วยังไม่มีโหนดไหนเลยที่เป็น centroid ได้ อันนี้จะรับประกันว่าโหนดที่เพิ่งเข้ามาใหม่นี่แหละที่เป็น centroid (จากการที่ทุก tree มี centroid 1-2 โหนด)
จะได้ว่ามีการเช็ก centroid โดยรวมประมาณ ครั้ง (ก็คือประมาณ 2 ครั้งต่อ 1 โหนด) ส่วนเวลาตอบคำถาม เราก็แค่สร้าง array มาเก็บไว้แล้วก็เรียกช่องนั้นตอบไปได้เลย
Time Complexity:
Memory Complexity:


